Week 1 Discussion Notes

Table of Contents

• Exponentials and Logarithms

  • Basic Properties
  • Change-of-Base Formula
  • Differentiation
  • Integration

• Logarithmic Differentiation

• Examples

Exponentials and Logarithms

Basic Properties

Definition

Let $b > 0$ and $b \neq 1$.

1. $b^x$ is called an exponential.
2. $\log_b{x}$ is called a logarithm.

The reason why we're avoiding $b = 1$ is because $1^x = 1$ for any $x$, which isn't interesting to us. Same thing for $b = 0$. Lastly, we don't want to deal with negative values of $b$ because we could end up with something like $\p{-1}^{1/2}$ which is an imaginary number, which is not covered in this class.

These functions have the following properties:

These properties should look pretty similar to each other to you. For example, the domain and range of the two functions are swapped, and the fourth line is "swapping addition and multiplication." This is because $b^x$ and $\log_bx$ are inverses:

Change-of-Base Formula

Proposition

Let $a, b > 0$ both be different from $1$. Then

$$\log_b{x} = \frac{\log_a{x}}{\log_a{b}}.$$

Proof.

The proof of this formula is good practice for using the properties of these functions. First, let $k = \log_b{x}$. Then because $b^x$ and $\log_b{x}$ are inverses,

$$b^k = b^{\log_b{x}} = x.$$

Then if we apply $\log_a{x}$ on both sides, we get

$$\begin{aligned} \log_a\p{b^k} &= \log_a{x} \\ \implies k\log_a{b} &= \log_a{x} \\ \implies k = \frac{\log_a{x}}{\log_a{b}}. \end{aligned}$$

$\square$

This is how I personally remember the formula: first, I remember very roughly what it looks like:

From here, I see that $b$ is below $x$ in the left-hand side, so it stays below in the end:

Differentiation

When $b = e$ (Euler's number), a lot of really nice things happen. For example,

$e$ is so important that $\log_e{x}$ has its own symbol: $\ln{x}$, which satisfies

Using the properties of exponentials and logarithms, we can use the facts above to find the derivative of $b^x$ for general values of $b$. Notice that $b = e^{\ln{b}}$, so

Then by the chain rule,

Similarly, if we use the change-of-base formula,

Integration

Since integration and differentiation are (almost) inverses, the fact that $\deriv{}{x} e^x = e^x$ tells us that

As before, we can use this fact to calculate the integral of any $b^x$:

Surprisingly, we can't integrate $\ln{x}$ with what we've learned yet. We'll learn later how to do it, but for now, just know that

Logarithmic Differentiation

Which is harder to differentiate, $e^x\sin{x}$ or $e^x + \sin{x}$? You (hopefully) said that the first one is harder, and that's because derivatives are easier with sums than with products.

The property that $\log_b\p{xy} = \log_b{x} + \log_b{y}$ is very useful for us because it turns the product into a sum, and we can use this (with the chain rule) to make some derivatives easier to compute.

Example 1.

Let $f\p{x} = e^x\sin{x}$. Use logarithmic differentiation to calculate $f'\p{x}$.

Solution.

Notice that

$$\begin{aligned} \ln{f\p{x}} &= \ln\p{e^x\sin{x}} \\ &= \ln{e^x} + \ln\p{\sin{x}} \\ &= x + \ln\p{\sin{x}}. \end{aligned}$$

Then by the chain rule, taking derivatives on both sides gives

$$\frac{f'\p{x}}{f\p{x}} = 1 + \frac{\cos{x}}{\sin{x}}.$$

Multiplying both sides by $f\p{x} = e^x\sin{x}$ then gives

$$f'\p{x} = e^x\sin{x} + e^x\sin{x} \cdot \frac{\cos{x}}{\sin{x}} = \boxed{e^x\sin{x} + e^x\cos{x}}.$$

Examples

Example 2.

Calculate $\displaystyle\deriv{}{x} \log_2{x}$.

Solution.

You could write down the derivative from the formulas, or if you don't remember it, you can use the change-of-base formula:

$$\begin{aligned} \deriv{}{x} \log_2{x} &= \deriv{}{x} \frac{\ln{x}}{\ln{2}} \\ &= \frac{1}{x\ln{2}}. \end{aligned}$$

Example 3.

Find the equation of the tangent line to $y = \log_2\p{1 + 4x^{-1}}$ at $x = 4$.

Solution.

To specify a line uniquely, you need two pieces of information: a point through the line and its slope. For a tangent line at $x = 4$, the line must pass through $\p{4, f\p{4}}$ with slope $f'\p{4}$. So, we need to calculate $f\p{4}$ and $f'\p{4}$:

$$f\p{4} = \log_2\p{1 + \frac{4}{4}} = \log_2\p{1 + 1} = \log_2{2} = 1.$$

For the derivative, we get

$$\begin{aligned} f'\p{x} &= \frac{1}{\p{1 + 4x^{-1}}\ln{2}} \cdot \deriv{}{x} \p{1 + 4x^{-1}} \\ &= \frac{1}{\p{1 + 4x^{-1}}\ln{2}} \p{-\frac{4}{x^2}} \\ \implies f'\p{4} &= \frac{1}{\p{1 + \frac{4}{4}}\ln{2}} \p{-\frac{4}{4^2}} \\ &= -\frac{1}{8\ln{2}}. \end{aligned}$$

So the tangent line passes through $\p{4, 1}$ and has slope $-\frac{1}{8\ln{2}}$, so if we use the point-slope formula, we get

$$\boxed{y - 1 = -\frac{1}{8\ln{2}}\p{x - 4}}.$$

Example 4.

Sketch the graph of $f\p{x} = x - \ln\p{x^2 + 1}$.

Solution.

Curve sketching is pretty hard to explain over text compared to during the live discussions. I'll explain my approach and give some resources to help you sketch it.

Before sketching, I like to calculate two sets of things:

1. The zeroes of $f'\p{x}$ (these are the critical points of $f$)
2. The zeroes of $f''\p{x}$ (these are the potential inflection points of $f$)

For (1), you get

$$\begin{aligned} f'\p{x} &= 1 - \frac{1}{x^2 + 1} \cdot \deriv{}{x} \p{x^2 + 1} \\ &= \frac{x^2 + 1}{x^2 + 1} - \frac{2x}{x^2 + 1} \\ &= \frac{\p{x - 1}^2}{x^2 + 1}. \end{aligned}$$

So the only zero of $f'$ is $x = 1$. For (2),

$$\begin{aligned} f''\p{x} &= \frac{\p{\deriv{}{x} \p{x - 1}^2} \p{x^2 + 1} - \p{x - 1}^2 \deriv{}{x} \p{x^2 + 1}}{\p{x^2 + 1}^2} \\ &= \frac{2\p{x - 1}\p{x^2 + 1} - 2x\p{x - 1}^2}{\p{x^2 + 1}^2} \\ &= \frac{2\p{x - 1}\br{\p{x^2 + 1} - x\p{x - 1}}}{\p{x^2 + 1}^2} \\ &= \frac{2\p{x - 1}\p{x^2 + 1 - x^2 + x}}{\p{x^2 + 1}^2} \\ &= \frac{2\p{x - 1}\p{x + 1}}{\p{x^2 + 1}^2} \end{aligned}$$

which gives $x = -1, 1$ as the potential inflection points. From here, you can figure out the signs of $f'$ and $f''$ everywhere:

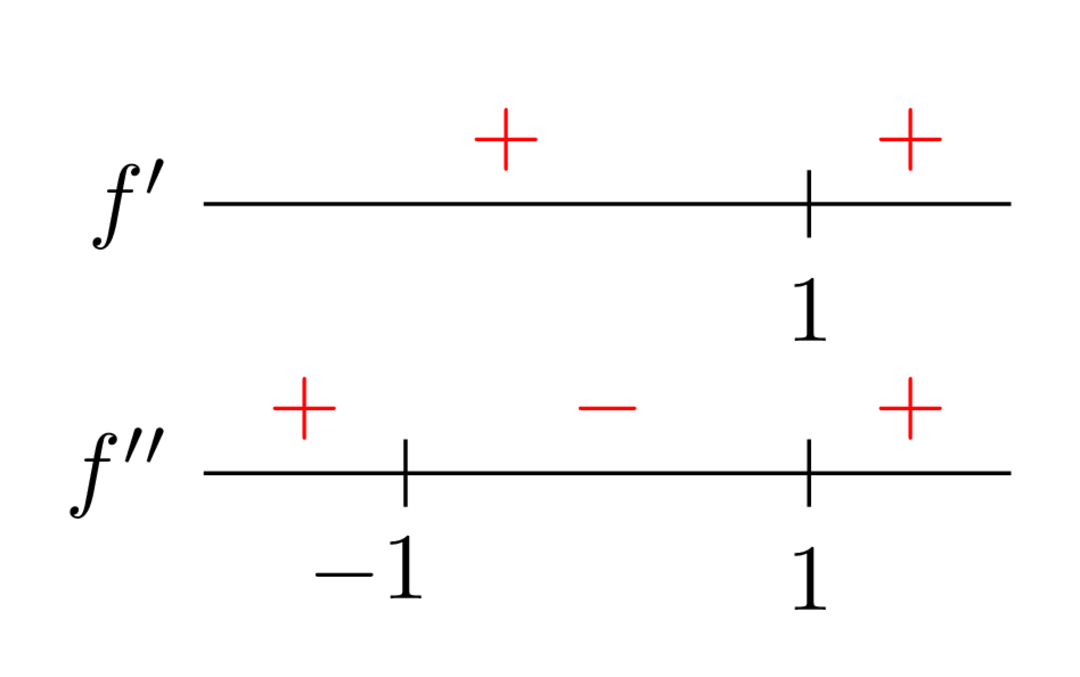
The sign of $f'$ tells you whether $f$ is increasing or decreasing, and the sign of $f''$ tells you whether you're concave up or concave down. You can look at these notes to see how the signs translate to the rough shape of $f$. You can also use Desmos to graph $f$ to check your answer.

Example 5.

Calculate $\displaystyle\int \frac{\diff{x}}{x\ln{x}}$.

Solution.

If $u = \ln{x}$, then $\diff{u} = \frac{1}{x} \,\diff{x}$, so the integral becomes

$$\begin{aligned} \int \frac{\diff{x}}{x\ln{x}} &= \int \frac{\diff{u}}{u} \\ &= \ln\abs{u} + C \\ &= \boxed{\ln\abs{\ln{x}} + C}. \end{aligned}$$

Example 6.

Calculate $\displaystyle\int \frac{\diff{x}}{x \p{\ln{x}} \ln\p{\ln{x}}}$.

Solution.

Similar to the previous one, we can let

$$u = \ln\p{\ln{x}} \implies \diff{u} = \frac{1}{x\ln{x}} \,\diff{x}.$$

Then

$$\begin{aligned} \int \frac{\diff{x}}{\p{x \ln{x}} \ln\p{\ln{x}}} &= \int \frac{\diff{u}}{u} \\ &= \ln\abs{u} + C \\ &= \boxed{\ln\abs{\ln\p{\ln{x}}} + C}. \end{aligned}$$