<Home>Teaching><MATH 31B (Fall 2020)>Week 1 Discussion Notes

Week 1 Discussion Notes

Table of Contents

Symbols

Here are a bunch of symbols that you'll probably see during lecture (and if you're a math major, for the rest of your life).

Definition
  • R= the set of real numbers =(−∞,∞)\mathbb{R} = \text{ the set of real numbers } = \p{-\infty, \infty}
  • ∈ =\in\: = "is in" or "is an element of"
  • ∃ =\exists\: = "there exists"
  • ∀ =\forall\: = "for all" or "for any" or "for every"
  •   ⟹   =\implies\: = "implies"
Example 1.

∃\exists water ∈\in my fridge

∀\forall student ∈\in MATH 31B, the student is an undergraduate

you are here   ⟹  \implies you ∈\in MATH 31B

you are here   ̸ ⁣ ⁣ ⁣  ⟹  \ \ \not\!\!\!\implies you are awake

Set Notation

You're probably familiar with intervals to specify sets (e.g., (a,b)\p{a, b}, [a,b]\br{a, b}, etc.). While these are useful, some sets may be hard or tedious to write as intervals, so we're going to introduce a new, more general way to specify sets.

Example 2.

{x∈R∣x≠0}=(−∞,0)∪(0,∞)=R∖{0}\set{x \in \R \mid x \neq 0} = \p{-\infty, 0} \cup \p{0, \infty} = \mathbb{R} \setminus \set{0}
Example 3.

The domain of f(x)=tan⁡xf\p{x} = \tan{x} is {x∈R∣x≠π2+πn, n is an integer}\set{x \in \R \mid x \neq \frac{\pi}{2} + \pi n,\ n \text{ is an integer}}.
Exercise 1.

Write {x∈R∣a<x and x≤b}\set{x \in \R \mid a < x \text{ and } x \leq b} as an interval.
Exercise 2.

Write the domain of f(x)=cot⁡xf\p{x} = \cot{x} using this notation.

Functions

A function ff always comains with a domain DD, and the range of ff is determined by DD. If the domain isn't specified, then it's usually taken to be the largest set where ff is defined.

Example 4.

If f(x)=1xf\p{x} = \frac{1}{x} and DD is not specified, then we assume D={x∈R∣x≠0}D = \set{x \in \R \mid x \neq 0}.
Example 5.

Let f(x)=x2f\p{x} = x^2.

  • D=R  ⟹  R=[0,∞)D = \R \implies R = \left[ 0, \infty \right)

  • D=[0,∞)  ⟹  R=[0,∞)D = \left[ 0, \infty \right) \implies R = \left[ 0, \infty \right)

  • D={x∈R∣x>2}  ⟹  R=(4,∞)D = \set{x \in \R \mid x > 2} \implies R = \p{4, \infty}

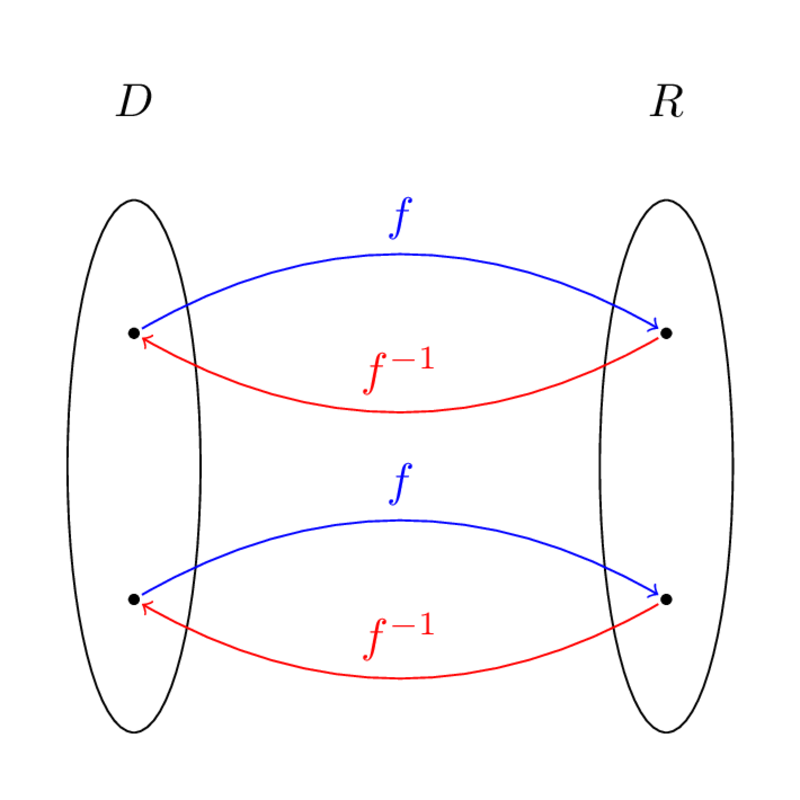
Inverses

What is an Inverse?

Given a function ff, we'd like to know if we can go "backwards" from ff. This is useful if you need to solve something like f(x)=yf\p{x} = y; if we can "undo" ff, then we automatically have the solution to the equation. This can be done if ff is invertible:

Definition

Let ff have domain DD and range RR. If ∃g\exists g with domain RR and range DD such that

  • f(g(x))=x∀x∈Rf\p{g\p{x}} = x\quad\forall x \in R and
  • g(f(x))=x∀x∈Dg\p{f\p{x}} = x\quad\forall x \in D,

then we say ff is invertible and we call f−1=gf^{-1} = g the inverse of ff.

When is there an Inverse?

So when does ff have an inverse? Let's look at a situation where ff does not have one.

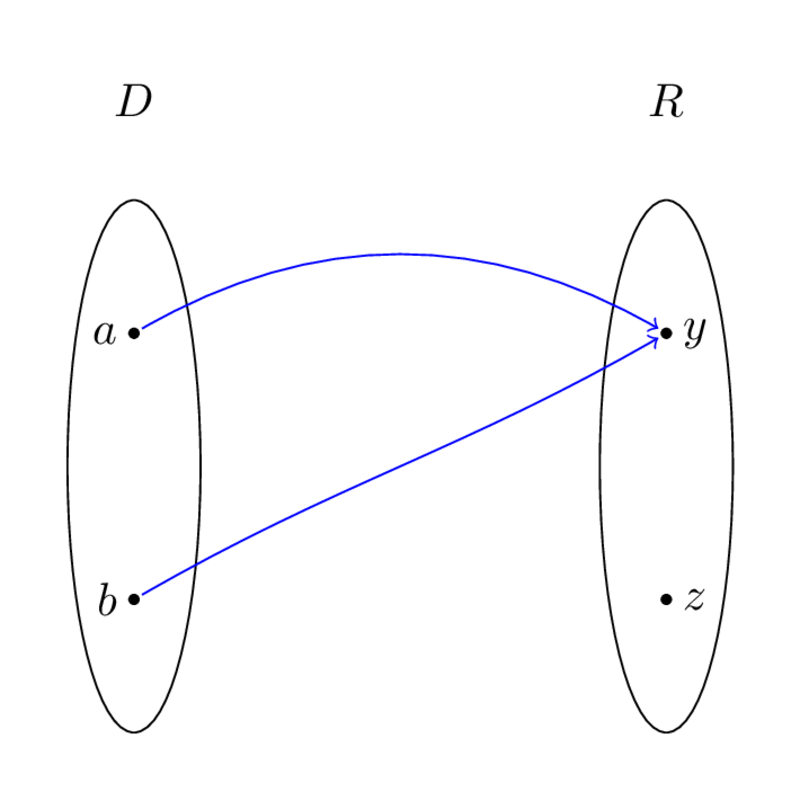
ff doesn't have an inverse here because we can't go backwards from yy to get both aa and bb. Indeed, any function gg with domain RR will map yy to either aa or bb, but not both. The problem is that ff maps two different elements to the same thing, so if we prevent this, ff will have an inverse.

To prevent this, we need ff to map two different elements to two different things. More succinctly, a≠b  ⟹  f(a)≠f(b)a \neq b \implies f\p{a} \neq f\p{b}. If ff satisfies this, then we call ff one-to-one, but this isn't the only way to tell if ff is one-to-one:

Definition (one-to-one)

Let ff have domain DD, and suppose one of the following is true about ff:

  • a≠b  ⟹  f(a)≠f(b) ∀a,b∈Da \neq b \implies f\p{a} \neq f\p{b}\ \forall a, b \in D or
  • f(x)=yf\p{x} = y has exactly one solution ∀y∈R\forall y \in R or
  • f(a)=f(b)  ⟹  a=b ∀a,b∈Df\p{a} = f\p{b} \implies a = b\ \forall a, b \in D or
  • ff passes the horizontal line test.

Then we say ff is one-to-one or injective.

Notice that the domain is very important when determining whether ff is one-to-one or not.

Example 6.

Let f(x)=x2f\p{x} = x^2.

  • If D=RD = \R, then ff is not one-to-one.

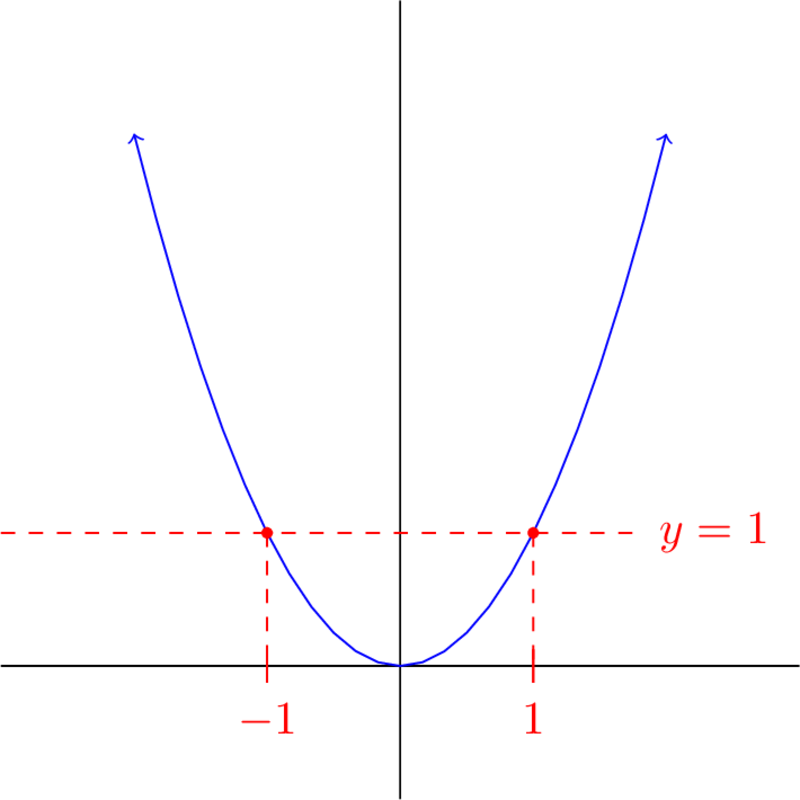
    f(x)=1f\p{x} = 1 has two solutions: −1-1 and 11.

  • If D=[0,∞)D = \left[ 0, \infty \right), then ff is one-to-one.

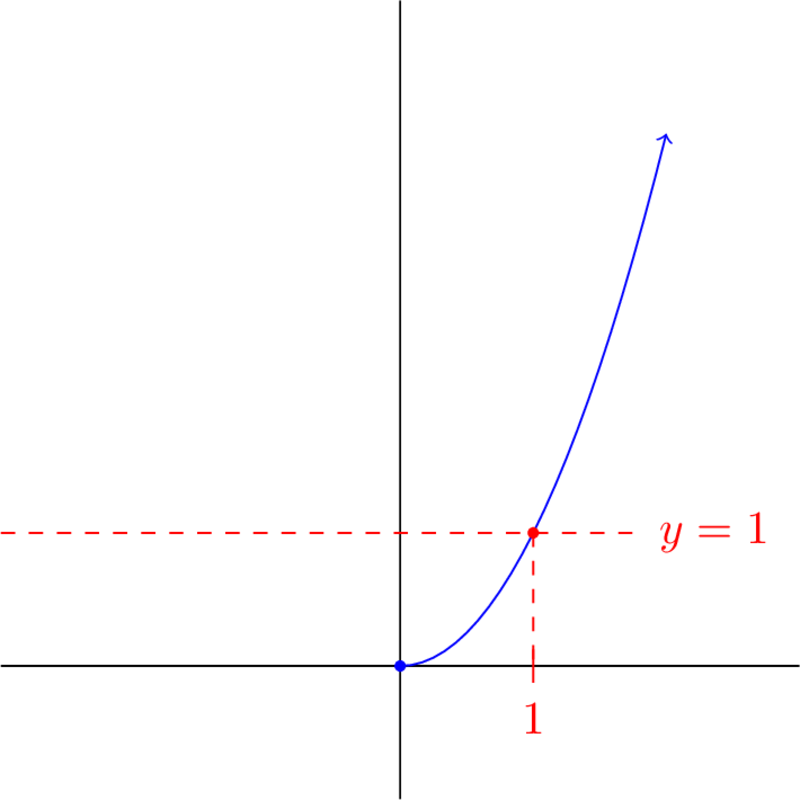
    Since ff is one-to-one, it has an inverse, which is f−1(x)=xf^{-1}\p{x} = \sqrt{x}.