<Home>Teaching><MATH 31B (Fall 2020)>Midterm 1 Solutions

Midterm 1 Solutions

Table of Contents

Question 1

True or false:

  1. The line tangent to f(x)=axf\p{x} = a^x at 00 has a slope equal to 11 for all a>0a > 0 and a≠1a \neq 1.
  2. The graph of the inverse function is the reflection of the graph of y=f(x)y = f\p{x} through the line y=0y = 0.
Solution.

(1) is false and (2) is false.

For (1), f′(x)=ln⁡(a)ax  ⟹  f′(0)=ln⁡(a)f'\p{x} = \ln\p{a} a^x \implies f'\p{0} = \ln\p{a}, which might not always be 11, e.g., a=4a = 4.

For (2), the graph of the inverse function is the reflection along the line y=xy = x, not y=0y = 0.

Question 2

Give one example of:

  1. A one-to-one and increasing function defined on the interval [−2,2]\br{-2, 2}.
  2. Two real-valued functions hh and ff such that h≪fh \ll f as x→∞x \to \infty.
Solution.

For (1), f(x)=xf\p{x} = x (restricted to [−2,2]\br{-2, 2}) works.

For (2), h(x)=1h\p{x} = 1 and f(x)=xf\p{x} = x works.

Question 3

Consider the function f(x)=1−x2x+1\displaystyle f\p{x} = \frac{\sqrt{1 - x^2}}{x + 1}.

  1. Find the largest domain on which ff is one-to-one and determine a formula for f−1f^{-1}.
  2. Find ddxf−1(1)\displaystyle \deriv{}{x} f^{-1}\p{1} using the definition of the derivative of f−1f^{-1} and (1).
Solution.

For (1), f(x)f\p{x} is only defined on (−1,1]\left\lparen -1, 1 \right\rbrack. On this domain, x>−1  ⟹  x+1>0x > -1 \implies x + 1 > 0, so

f′(x)=−x(1−x2)−1/2(x+1)−1−x2(x+1)2=−x(x+1)−(1−x2)(x+1)21−x2=−x+1(x+1)21−x2<0.\begin{aligned} f'\p{x} &= \frac{-x\p{1 - x^2}^{-1/2}\p{x + 1} - \sqrt{1 - x^2}}{\p{x + 1}^2} \\ &= \frac{-x\p{x + 1} - \p{1 - x^2}}{\p{x + 1}^2\sqrt{1 - x^2}} \\ &= -\frac{x + 1}{\p{x + 1}^2\sqrt{1 - x^2}} < 0. \end{aligned}

So, f(x)f\p{x} is strictly decreasing on this interval, which means that it's one-to-one on (−1,1]\left\lparen -1, 1 \right\rbrack.

For the inverse:

x=1−y2y+1xy+x=1−y2x2y2+2x2y+x2=1−y2(x2+1)y2+2x2y+(x2−1)=0.\begin{aligned} x &= \frac{\sqrt{1 - y^2}}{y + 1} \\ xy + x &= \sqrt{1 - y^2} \\ x^2y^2 + 2x^2y + x^2 &= 1 - y^2 \\ \p{x^2 + 1}y^2 + 2x^2y + \p{x^2 - 1} &= 0. \end{aligned}

To solve for yy, you can use the quadratic formula, so there are two possibilities:

y=−2x2±4x4−4(x2+1)2(x2+1)=−2x2±22x2+2=1−x21+x2or−1.y = \frac{-2x^2 \pm \sqrt{4x^4 - 4\p{x^2 + 1}}}{2\p{x^2 + 1}} = \frac{-2x^2 \pm 2}{2x^2 + 2} = \frac{1 - x^2}{1 + x^2} \quad\text{or}\quad -1.

The domain of f(x)f\p{x} doesn't include −1-1, so −1-1 is not possible. Thus,

f−1(x)=1−x21+x2.f^{-1}\p{x} = \boxed{\frac{1 - x^2}{1 + x^2}}.

For (2), there's the formula

(f−1)′(1)=1f′(f−1(1))=1f′(0)=−1.\p{f^{-1}}'\p{1} = \frac{1}{f'\p{f^{-1}\p{1}}} = \frac{1}{f'\p{0}} = \boxed{-1}.

I calculated f′(x)f'\p{x} above.

Question 4

A population is modeled by a function P=P(t)P = P\p{t}. Initially, the population counts 10001000. The rate of change of the population is proportional to PP. Find the population at time t=17t = 17 years given that the doubling time is 88 years.

  1. Explain your solving process step-by-step without doing any computation.
  2. Show full work.
Solution.

I will omit (1).

If the rate of change of the population is proportional to PP, then PP satisfies P′=kPP' = kP for some constant kk. This means that P(t)=P0ektP\p{t} = P_0 e^{kt}. We're given that the initial population is 10001000, so P(0)=P0=1000P\p{0} = P_0 = 1000. The doubling time is 88 years, which means that after 88 years, the population doubles to 20002000, so

P(8)=1000e8k=2000  ⟹  e8k=2  ⟹  k=ln⁡28.P\p{8} = 1000 e^{8k} = 2000 \implies e^{8k} = 2 \implies k = \frac{\ln{2}}{8}.

Plugging everything in,

P(17)=1000e17(ln⁡2)/8≈4362.P\p{17} = 1000 e^{17\p{\ln{2}}/8} \approx \boxed{4362}.

Question 5

Find the limits using L'Hôpital's rule.

  1. lim⁡t→1(t−1)ln⁡(1(t−1)2)\displaystyle \lim_{t\to1} \p{t - 1}\ln\p{\frac{1}{\p{t - 1}^2}}.
  2. lim⁡x→0sin⁡−1(2x)3x\displaystyle \lim_{x\to0} \frac{\sin^{-1}\p{2x}}{3x}.
Solution.

(1) is of the form 0⋅∞0 \cdot \infty, so

lim⁡t→1[(t−1)ln⁡(1(t−1)2)]=lim⁡t→1ln⁡(1(t−1)2)1t−1=lim⁡t→1−2ln⁡(t−1)1t−1=Hlim⁡t→1−2t−1−1(t−1)2=lim⁡t→12(t−1)=0.\begin{aligned} \lim_{t\to1} \br{\p{t - 1}\ln\p{\frac{1}{\p{t - 1}^2}}} &= \lim_{t\to1} \frac{\ln\p{\frac{1}{\p{t - 1}^2}}}{\frac{1}{t - 1}} \\ &= \lim_{t\to1} \frac{-2\ln\p{t - 1}}{\frac{1}{t - 1}} \\ &\overset{H}{=} \lim_{t\to1} \frac{-\frac{2}{t - 1}}{-\frac{1}{\p{t - 1}^2}} \\ &= \lim_{t\to1} 2\p{t - 1} \\ &= \boxed{0}. \end{aligned}

(2) has the form 00\displaystyle \frac{0}{0}, so we can use L'Hôpital's directly:

lim⁡x→0sin⁡−1(2x)3x=Hlim⁡x→021−4x23=lim⁡x→0231−4x2=23.\lim_{x\to0} \frac{\sin^{-1}\p{2x}}{3x} \overset{H}{=} \lim_{x\to0} \frac{\frac{2}{\sqrt{1 - 4x^2}}}{3} = \lim_{x\to0} \frac{2}{3\sqrt{1 - 4x^2}} = \boxed{\frac{2}{3}}.

Question 6

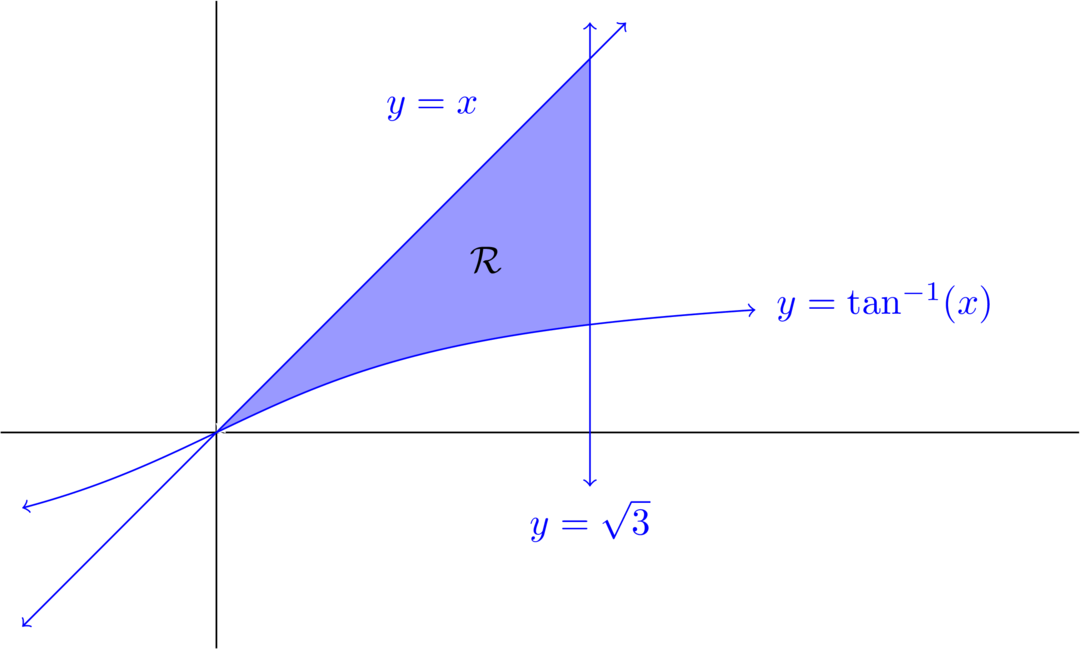
Consider the region R\mathcal{R} enclosed by y=tan⁡−1xy = \tan^{-1}{x}, y=xy = x, x=0x = 0, and x=3x = \sqrt{3}.

  1. Sketch the region R\mathcal{R}.
  2. Find the area of R\mathcal{R}.
Solution.

For (1), the region looks like

So for (2), you get

∫03x−tan⁡−1x dx.\int_0^{\sqrt{3}} x - \tan^{-1}{x} \,\diff{x}.

To calculate ∫tan⁡−1x dx\int \tan^{-1}{x} \,\diff{x}, you can integrate by parts with u=tan⁡−1xu = \tan^{-1}{x} and dv=dx\diff{v} = \diff{x}, which gives

du=dx1+x2 dxandv=x.\diff{u} = \frac{\diff{x}}{1 + x^2} \,\diff{x} \quad\text{and}\quad v = x.

So,

∫tan⁡−1x dx=xtan⁡−1x−∫x1+x2 dx=xtan⁡−1x−12ln⁡(1+x2)+C.\int \tan^{-1}{x} \,\diff{x} = x\tan^{-1}{x} - \int \frac{x}{1 + x^2} \,\diff{x} = x\tan^{-1}{x} - \frac{1}{2}\ln\p{1 + x^2} + C.

The area is then given by

∫03x−tan⁡−1x dx=(x22−xtan⁡−1x+12ln⁡(1+x2))∣03=32−3tan⁡−13+12ln⁡4=32−π33+ln⁡222=9−2π36−ln⁡2.\begin{aligned} \int_0^{\sqrt{3}} x - \tan^{-1}x \,\diff{x} &= \left. \p{\frac{x^2}{2} - x\tan^{-1}{x} + \frac{1}{2}\ln\p{1 + x^2}} \right\rvert_0^{\sqrt{3}} \\ &= \frac{3}{2} - \sqrt{3}\tan^{-1}\sqrt{3} + \frac{1}{2}\ln{4} \\ &= \frac{3}{2} - \frac{\pi\sqrt{3}}{3} + \frac{\ln{2^2}}{2} \\ &= \boxed{\frac{9 - 2\pi\sqrt{3}}{6} - \ln{2}}. \end{aligned}