Problem 2
Prove that the eigenvalues of an upper-triangular matrix are its diagonal entries.
b) Give an example of a matrix which is not diagonalizable over
Problem 3
Prove that a linear operator on an 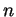 -dimensional vector space which has
-dimensional vector space which has
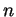 distinct eigenvalues is diagonalizable.
distinct eigenvalues is diagonalizable.
Problem 4
Prove that if 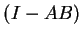 for
for
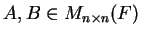 is invertible,
then so is
is invertible,
then so is 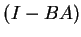 , and
, and
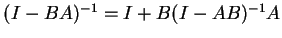 . (You might
want to use this result in problem 6 on page 106).
. (You might
want to use this result in problem 6 on page 106).
Problem 5
Let
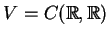 be the vector space of all continuous
real-valued functions on the real line. Prove that the operator
be the vector space of all continuous
real-valued functions on the real line. Prove that the operator 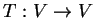 given by
given by
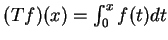 has no eigenvalues.
has no eigenvalues.
Problem 6
a) Give a matrix (with real entries) which is diagonalizable over
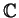 ,
but is not diagonalizable over
,
but is not diagonalizable over
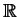 .
.
(Hint: in both parts, it can be useful to think first about an operator with such properties).