Problem 2
Let 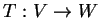 be a linear transformation.
be a linear transformation.
a) (Rank-Nullity Theorem) If
b) Give an example of an infinite-dimensional vector space ![]() and a linear
operator
and a linear
operator ![]() on
on ![]() such that the statement of the rank-nullity theorem
is false. Return to your proof of this theorem and think why it does not work
in the infinite-dimensional case.
such that the statement of the rank-nullity theorem
is false. Return to your proof of this theorem and think why it does not work
in the infinite-dimensional case.
Problem 3
Prove that a linear transformation is one-to-one iff its null space consists
of the zero vector only.
Problem 4
Prove that a linear transformation 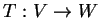 , where
, where 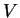 and
and 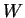 are finite-dimensional vector spaces with
are finite-dimensional vector spaces with
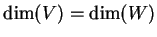 ,
is one-to-one if and only if
,
is one-to-one if and only if
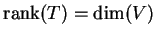 . (Hint:
first, prove that it is one-to-one iff it is onto; then prove that it is onto
iff
. (Hint:
first, prove that it is one-to-one iff it is onto; then prove that it is onto
iff
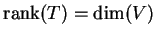 ).
).