

Math 115AH Homework # 2
(additional problems)
Problem 1
Let
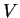
be a vector space which is spanned by a finite set
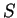
consisting
of
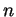
elements. Show that
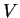
is finite-dimensional with dimension
less then or equal to
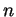
. (You should not assume from the beginning that
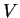
is finite-dimensional!)
Problem 2
a) Let
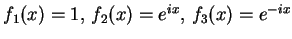
. Prove that
these functions are linearly independent in the space
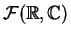
of all complex-valued functions on the real line.
b) Let
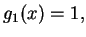
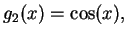
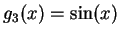
.
Find an invertible
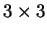
matrix such that
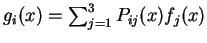
for all
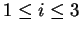
.
Problem 3
Let
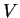
be a
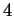
-dimensional vector space, and
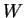
be its
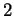
-dimensional
subspace. Show that there is a
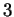
-dimensional subspace
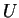
of
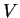
such that
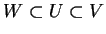
.
Problem 4
Let
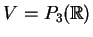
,
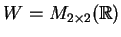
be two
vector spaces, both of dimension
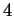
. Construct an explicit isomorphism
from
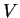
to
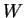
.
Problem 5
a) Prove that a linear map
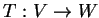
is an isomorphism iff it sends a
basis of
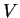
to a basis of
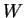
.
b) Let
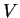
and
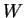
be vector spaces, and let
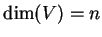
.
Let
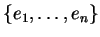
be a basis in
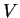
and
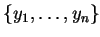
be an arbitrary set of vectors in
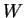
. Prove (by giving an explicit construction)
that there exists a linear transformation
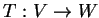
such that
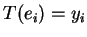
for all
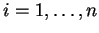
. Is such a transformation unique?
Problem 6
(Annihilators) Let
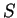
be a subset of a vector space
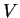
.
- Prove that its annihilator
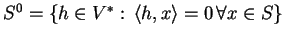 is a subspace of
is a subspace of 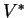 .
.
- Prove that if
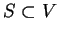 is a subspace and
is a subspace and 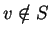 , then there
exists
, then there
exists
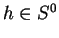 such that
such that
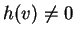 .
.
- Let
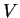 be finite-dimensional and
be finite-dimensional and
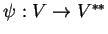 be the isomorphism
defined by
be the isomorphism
defined by
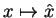 , where
, where
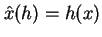 for all
for all
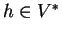 .
Prove that
.
Prove that
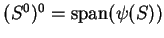 . In particular, if
. In particular, if 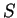 is a subspace, conclude that
is a subspace, conclude that
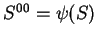 (i.e.,
(i.e., 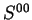 and
and
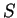 can be identified by the natural isomorphism between
can be identified by the natural isomorphism between 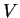 and
and 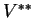 ).
).
- Let
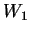 and
and 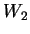 be subspaces. Show that
be subspaces. Show that
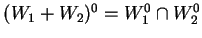 and
and
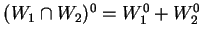 . (Hint: first prove
that
. (Hint: first prove
that
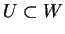 implies that
implies that
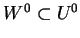 ).
).
Math 115AH Homework # 2
This document was generated using the
LaTeX2HTML translator Version 99.2beta6 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /u/sonia/h3/guest/radko/Teaching/math115ah/homework/hw2.tex
The translation was initiated by Olga Radko on 2003-08-04


Olga Radko
2003-08-04
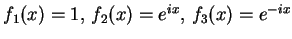 . Prove that
these functions are linearly independent in the space
. Prove that
these functions are linearly independent in the space
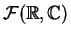 of all complex-valued functions on the real line.
of all complex-valued functions on the real line.
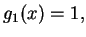
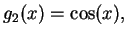
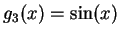 .
Find an invertible
.
Find an invertible 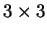 matrix such that
matrix such that
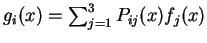 for all
for all
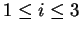 .
.
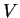 be a
be a 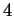 -dimensional vector space, and
-dimensional vector space, and 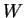 be its
be its 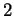 -dimensional
subspace. Show that there is a
-dimensional
subspace. Show that there is a 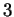 -dimensional subspace
-dimensional subspace 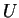 of
of 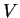 such that
such that
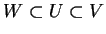 .
.
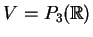 ,
,
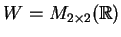 be two
vector spaces, both of dimension
be two
vector spaces, both of dimension 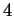 . Construct an explicit isomorphism
from
. Construct an explicit isomorphism
from 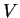 to
to 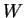 .
.
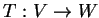 is an isomorphism iff it sends a
basis of
is an isomorphism iff it sends a
basis of 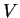 to a basis of
to a basis of 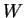 .
.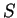 be a subset of a vector space
be a subset of a vector space 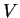 .
.