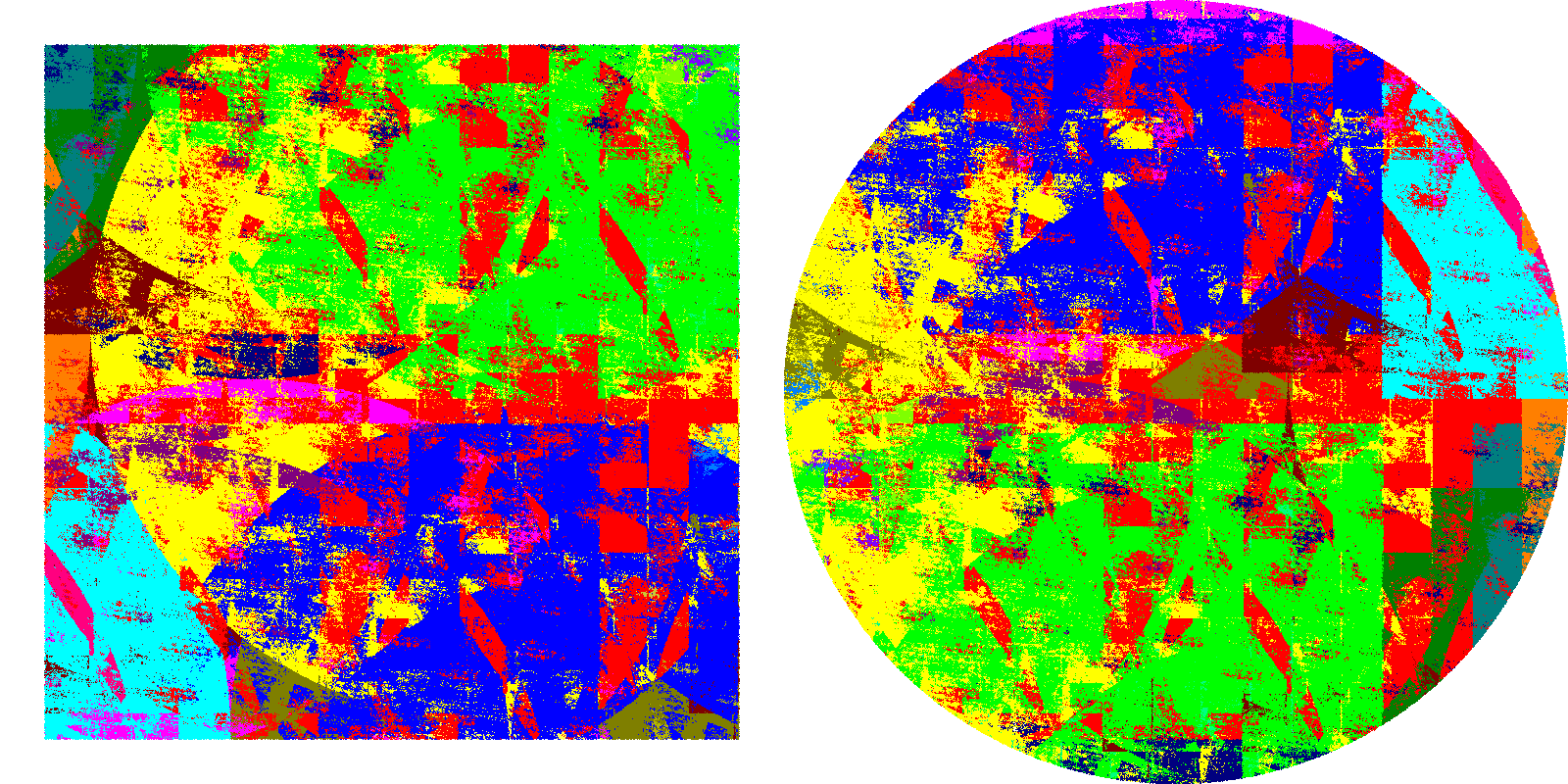
Pictures of Borel Circle Squaring
The images below show the first step in the proof there is a Borel solution to Tarski's circle squaring problem. We give three bounded real-valued function defined on the torus. Their sum is the characteristic function of a square. However, after translating these functions by the vectors shown, they sum to the characteristic function of a circle.
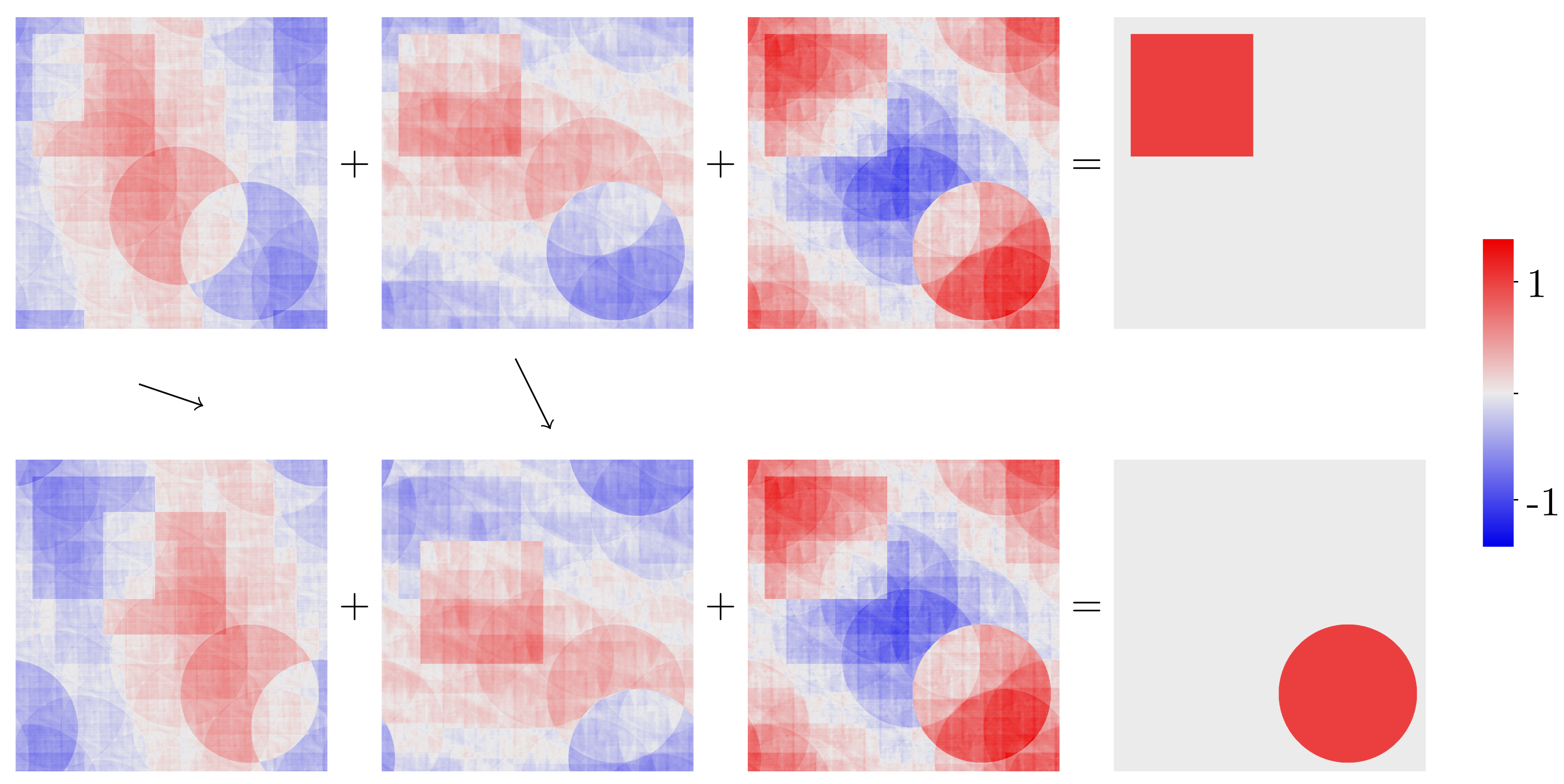
(Click on the picture to enlarge)
These functions were calculated using the formulas in Section 4 of our paper "Borel circle squaring". Section 5 of the paper describes how to convert such real-valued functions to integer-valued functions with the same property. From these integer valued functions, it is easy to find an equidecomposition of a circle and a square (see Section 6).
Click here for a video.
The methods used in Sections 5 and 6 are quite complicated and yield an equidecomposition with a large number of pieces (about 10^200 pieces). So it is not possible to make a picture of an explicit equidecomposition from them. However, computer experimentation has suggested (but not proven) that the problem should be solvable with a quite small number of pieces. For example, below is a picture of an "pixel-level" equidecomposition using 22 pieces. It would be reasonable to conjecture that the algorithm used to make this picture works at all points of the circle and square to make an equidecomposition with 22 pieces. However, we have not proven this.