Grace Li

On social media, there tend to be individual accounts that initiate conversations, posts or other content more frequently. These heterogeneous levels of activity can impact the visibility of online content and what goes “viral”. However, existing research on models of opinion dynamics tends to focus on uniform probability distributions of activity. I developed a generalization of the Deffuant–Weisbuch bounded-confidence model of opinion dynamics that uses node weights to model agents in a social network with different probabilities of interacting. Using numerical simulations, I systematically investigated the effects of node weights and demonstrated that introducing them results in longer convergence times and more opinion fragmentation than in a baseline DW model. I also seek to apply my models to real-world social networks and to discover measures of social influence of nodes that account for both their node weight (representing sociability) and their position in a social network. My models are applicable to understanding the mechanisms in the spread of misinformation and disinformation, as well as identifying key individuals in this process and mitigating their harmful effects.

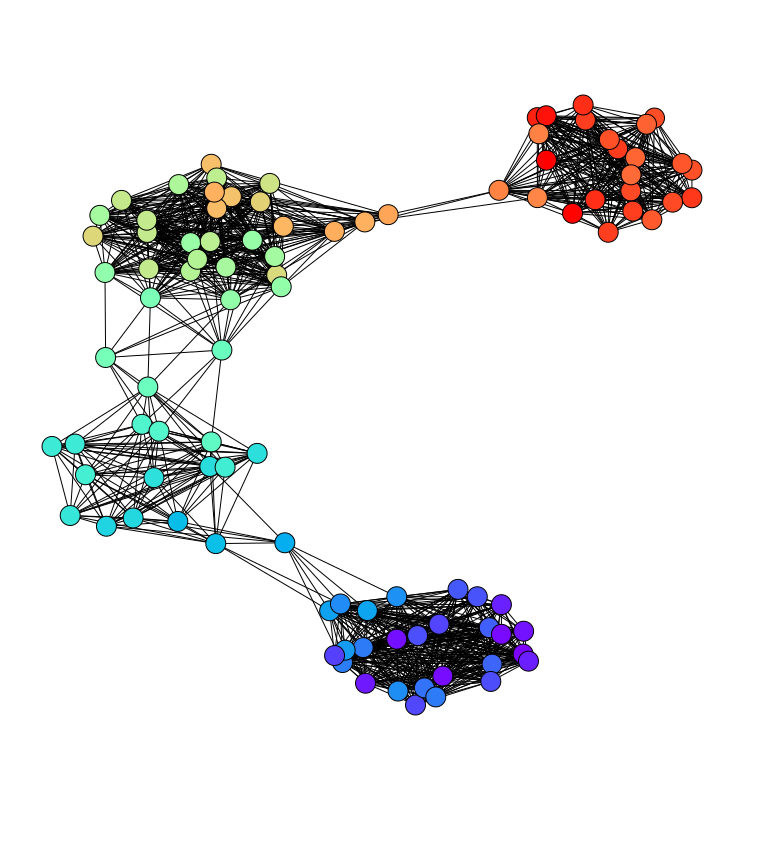
The ways that we form and change our opinions are influenced heavily by our social interactions. How much other people can influence us depends on many factors including the past interactions and levels of trust. In bounded-confidence models of opinion dynamics, pairs of agents only influence each other if their opinions differ by less than some “confidence bound” between them. We generalize the Hegselmann–Krause and Deffaunt–Weisbuch bounded-confidence models to incorporate adapative confidence bounds. This models time-dependence in the willingness of agents to listen to each other based on the nature of their prior interactions. We analytically and numerically explore the limiting behaviors of our models, including the confidence-bound dynamics, the formation of opinion clusters, and the time evolution of the time-dependent subgraph of the network with edges only between nodes that can currently influence each other. For a wide range of parameters, our models tend to yield less opinion fragmentation. We also observe novel consensus behaviors not present in the baseline Hegselmann–Krause and Deffaunt–Weisbuch models.

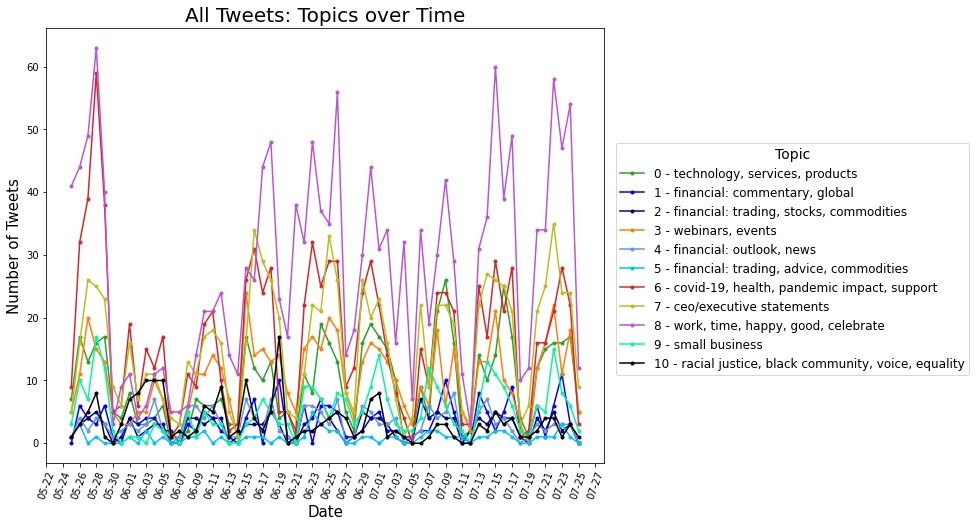
The summer of 2020 saw a marked increase in public expression of support for the Black Lives Matter (BLM) movement. As the movement gained momentum online, corporations faced social pressure to respond. We examined the relevant Twitter activity of Fortune 100 companies during this time period by analyzing the content of their tweets (data from Kevin McElwee), possible underlying networks between the companies, and patterns in their responses. I focused on topic analysis of the Fortune-100 tweets using non-negative matrix factorization (NMF). I identified topics including CEO statements, the COVID-19 pandemic, racial justice, celebrations, and investing, as well as which companies were most prominent (both in terms of number of tweets and user engagement) in those Twitter conversations. Using NMF on weekly time intervals and matching topics, I identified shifts over time for each topic. For example, the CEO statements shifted focus between addressing systemic racism, diversity, 2nd quarter earnings, and sustainability.

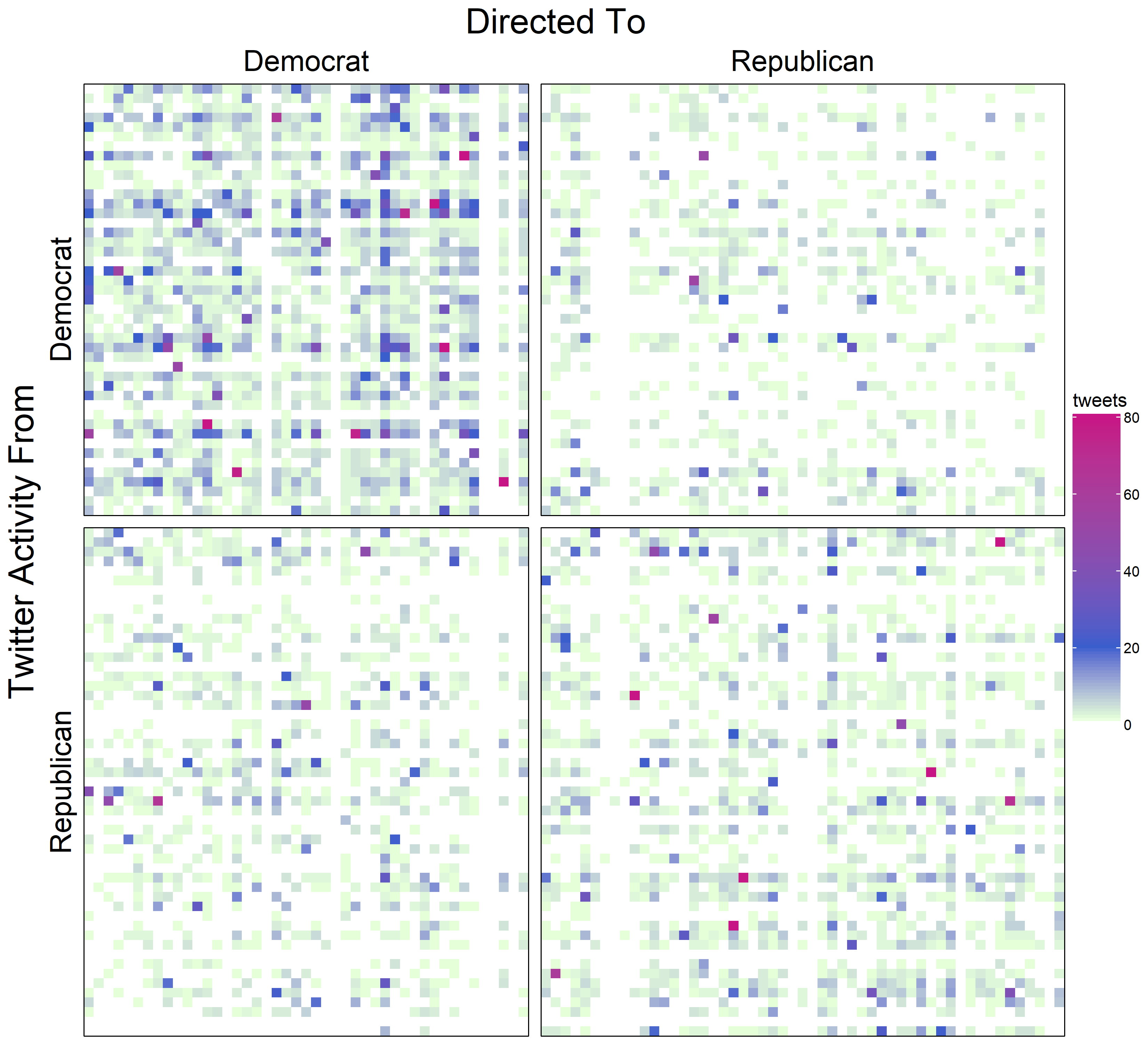
In the past decade, Twitter has become a popular platform for legislators to publicize their activities and views. To analyze the social forces influencing public online interactions between legislators, I constructed a network of senators in the 116th Senate with edges representing their interactions on Twitter. Using centrality measures from social network analysis, I identified central figures in the Twitter network. While some of the key senators held additional positions of power, many did not. Using exponential random graph models (ERGMs), I characterized the partisan influence on the network and found that the minority Democratic Party was more active on Twitter and a full nodemix ERGM model is needed for best fit of the partisan effects. Additional dyadic influences on the Senate network were reciprocity of ties, homophily for geographic region, and tendency to tweet those of similar age. I also considered the Democrat and Republican sub-networks separately to find within-party influences. Older Democrats tended to have more ties, while younger Republicans tended to have more ties. The Republicans also had significant region-based homophily and propensity for ties among senators with closer NOMINATE-1 scores representing voting-record partisanship. Both the Democrats and Republicans had a propensity to form transitive triads.

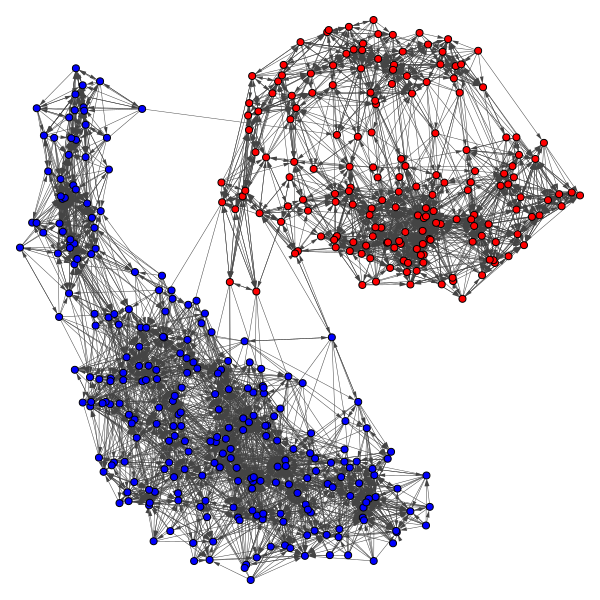
We utilized voting records in conjunction with clustering and community-detection algorithms to classify legislators into clusters by political stance. The underlying assumption is that legislators with more similar voting records have more similar political stances. We considered legislatures from multiple countries: the United States House of Representatives, German Bundestag, Legislative Council of Hong Kong, and South Korean National Assembly. For each legislature, we assessed how well different combinations of similarity functions and clustering algorithms could detect existing, known political parties. We were able to identify what larger political-party coalitions the independent legislators with no party affiliation were most aligned with. Additionally, we saw that number of clusters and modularity of the graph communities can be used to detect unity or division within a political party, and when there may be a shift in power within the legislature. In this project, I focused on investigating the use of different similarity functions to place legislators in a network with distances calculated from similarity of the roll-call votes.