


Next: o_projs32
Up: o_projs32
Previous: o_projs32
0. The setup
There are three ingredients: A viewplane, an object, and a viewpoint,
which can be at infinity. The viewplane is often taken to be the
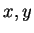 -plane.
-plane.
There are several versions:
#1: A right-handed coordinate system with the viewplane thought of
as horizontal. This is the usual picture from calculus. The viewpoint
is regarded as being in the positive 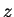 -direction.
-direction.
#2: A right-handed coordinate system with the viewplane thought of
as vertical, as it would be if the 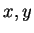 -plane is a display screen.
The viewpoint is regarded as being in the positive
-plane is a display screen.
The viewpoint is regarded as being in the positive 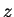 -direction.
-direction.
#3: A left-handed coordinate system with the viewplane thought of
as vertical. The viewpoint is regarded as being in the negative 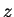 -direction.
-direction.
Notes.
- (a)
- The first two versions are exactly the same mathematically!
The same computer program would give correct output for each.
- (b)
- It doesn't really matter whether the object is on the same side of
the viewplane as the viewpoint, or on the opposite side, or straddling it.
A formula valid for one case works for the other; it's just that points
of the object may have positive
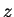 -values in one case and negative in
another.
-values in one case and negative in
another.
- (c)
- With a left-handed coordinate system, the algebraic computation of
cross products stays the same, while the geometric meaning of the cross
product obeys the left-hand rule instead of the right-hand rule.
- (d)
- If the viewpoint is at infinity, we usually think of it as being
on one side of the viewplane or the other, even though in
P
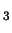 it doesn't really make a difference. Otherwise, we couldn't talk later
about hidden lines and faces.
it doesn't really make a difference. Otherwise, we couldn't talk later
about hidden lines and faces.
- (e)
- Although we usually talk about ``an object'', of course the
object could be a whole complicated scene with many parts.
- (f)
- For the present, we ignore the issue of hidden lines and faces,
which is quite complicated when you analyze it in detail. Solids,
then, can be wire-frame figures, where only edges are given and
faces are not filled in.
- (g)
- The viewpoint and viewplane are often called the center of projection
and the projection plane.



Next: o_projs32
Up: o_projs32
Previous: o_projs32
Kirby A. Baker
2002-01-28
![]() -plane.
-plane.
![]() -direction.
-direction.
![]() -plane is a display screen.
The viewpoint is regarded as being in the positive
-plane is a display screen.
The viewpoint is regarded as being in the positive ![]() -direction.
-direction.
![]() -direction.
-direction.