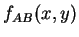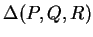Study Guide

In addition to the general topics listed below, be able to do all homework problems, including those ``not to hand in''. In general, where formulas are developed you should know them, and if there is a proof in a homework problem you should know it. The exam will cover the whole course, but will have an extra emphasis on topics past the midterm.

Review of vectors and linear transformations

• The projection of a vector on a line
• Cross products
• Relation to matrices; ``mapping the house''; determinants; invertibility

Orthogonal matrices and transformations

• Meaning and characterization of orthogonal matrices
• Rotation matrices
• Reflections--enough to do homework problems
• ``Three-step'' method for problems

Affine transformations

• Affine transformations
• Extended matrices
• Preservation properties
• Mapping triangles and parallelograms
• Idea of mapping a standard object of any sort
• ``Hidden explanation'' (see under homogeneous too)
• Applications to windowing, area of triangle, volumes

Homogeneous coordinates and the real projective plane

• Homogeneous coordinates
• Projective transformations
• Points at infinity
• The real projective plane
• Geometry of the real projective plane
• Making projective transformations
• How much freedom?
• How to make a specific quadrangle go to a specific quadrangle.
• Three-dimensional projective space
• Affine transformations as projective transformations
• The ``hidden'' or ``secret'' explanation using hlt's in one dimension higher

Projections from three dimensions to two

• The setup and main classification
• Characteristics of the main types
• How to calculate projections
• Projections on a slanted viewplane
• Kinds of perspective projections--how to recognize
• Subclassifications and how to recognize them, whether given as a picture or given by an algebraic description of the object, viewpoint, and viewplane.
• Rotating given latitude/longitude to north pole. Be clear on which is latitude and which is longitude!

Convex sets and convex polyhedra

• Convexity
• The convex hull of a set
• Convex combinations
• Convex polyhedra
• Hidden-surface removal for convex polyhedra

Interpolation for polynomial parametric curves

• Parametric curves in general; polynomial curves
• Polynomial curves
• Lagrange interpolation (concepts; basis functions)
• Properties of polynomials

Cubic Bézier curves

• Definitions of Bernstein and Bézier
• Properties of the cubic Bernstein polynomials and Bézier curves. Know those that were used in homework or mentioned in lecture.
• Applications: loops, arcs, arrows, S-curve, Hermite
• Derivative theorem for Bézier curves (of any degree).

Cubic spline curves

• Bézier curves with zero second derivative at one end
• Gluing two Bézier curves; A-frames
• B-spline curves and their construction
• Interpolation by splines
• Basis functions, how to calculate
• (Skip other possible end conditions and non-uniform spline curves)
• Applications to animation

Parametric Surfaces

• Parametric curves and surfaces
• Ruled surfaces; bilinear patch (know)
• (Coons patch-don't need to know)
• Tensor bases
  • for interpolated spline surfaces
  • for Lagrange surfaces
  • (not for Bézier surfaces, even though that was on homework)
• How to invent parametric surfaces, as in lab assignment
• Isoparametric curves
• Normal vector at a point

Ray-tracing

• The setup and its ingredients
• Tracing a ray for a given pixel
• Phong shading
• (not mirror reflection)

Linear geometry

• Ways of expressing lines in R$^ 2$
• Relational form and applications
• Relational form
• $f _ {AB}(x,y)$
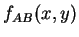
• How to tell whether two line segments cross , and where
  • $\Delta(P,Q,R)$
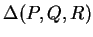
  • Two-point relational formula
  • Crossing of lines, line segments
  • Points inside/outside triangles, convex polygons
  • Points inside non-convex polygons--if discussed

Labs -- Look them over.