


Next: m_hcoords
Up: m_hcoords
Previous: m_hcoords
8. Three-dimensional projective space
All the ideas discussed above can be adapted to
three-dimensional space. An overview:
- (1)
- Homogeneous coordinates are
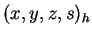 . The names of
each point differ by nonzero scalar factors.
. The names of
each point differ by nonzero scalar factors.
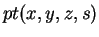 is an ordinary point if
is an ordinary point if 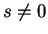 and is a point at infinity if
and is a point at infinity if
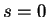 .
.
- (2)
- Each point at infinity corresponds to a family of parallel
lines in
R
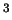 . These lines meet in
P
. These lines meet in
P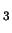 at their point
at infinity.
at their point
at infinity.
(In
R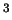 , two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)
, two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)
- (3)
- Real projective 3-space
P
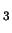 consists of
R
consists of
R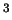 together with points at infinity.
together with points at infinity.
- (4)
- A projective transformation
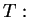 P
P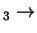 P
P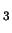 is a
transformation obtained by multiplying the homogeneous
coordinates of each point by a nonsingular
is a
transformation obtained by multiplying the homogeneous
coordinates of each point by a nonsingular
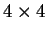 matrix
matrix
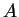 .
.
- (5)
- Five points in
P
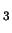 are said to be in general position
if no four are coplanar. If
are said to be in general position
if no four are coplanar. If
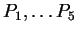 are in general
position and
are in general
position and
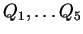 are in general position, then there
exists a projective transformation
are in general position, then there
exists a projective transformation
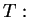 P
P P
P such
that
such
that
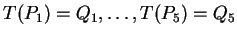 .
.



Next: m_hcoords
Up: m_hcoords
Previous: m_hcoords
Kirby A. Baker
2002-01-23
![]() , two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)
, two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)
![]() , two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)
, two lines are parallel if they lie in the same
plane and do not intersect. Two lines that do not intersect and
do not lie in the same plane are said to be skew.)