


Next: ii_ray_tr
Up: ii_ray_tr
Previous: ii_ray_tr
2. Variations
- If there are several objects, it is necessary to see where the
ray hits them all, mathematically, and then take
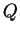 to be the
first hit (lowest
to be the
first hit (lowest 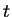 ). If the surface at
). If the surface at 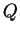 is diffusely
reflective, you have to trace the ray from
is diffusely
reflective, you have to trace the ray from 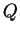 in the direction
of the light source to see if hits another object (so
in the direction
of the light source to see if hits another object (so 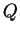 would be
in a shadow).
would be
in a shadow).
- If one or more objects are not convex, then it is possible
that
n
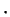 s could be positive at
s could be positive at 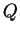 and yet the ray
from
and yet the ray
from 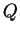 to the light source could hit another part of the same object,
so you need to check for that too.
to the light source could hit another part of the same object,
so you need to check for that too.
- If the surface of the object is specular-reflective
(mirror-like) at
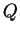 , then it is necessary to bounce the ray
off it by using the law of reflection (which involves the ray
direction and
n). Then follow that ray for possible
reflections off other objects, and so on, until you get to a
diffusely reflective surface.
, then it is necessary to bounce the ray
off it by using the law of reflection (which involves the ray
direction and
n). Then follow that ray for possible
reflections off other objects, and so on, until you get to a
diffusely reflective surface.
- A transparent medium such as glass partly reflects and partly
refracts. The proportions of each depend on the angle of incidence.
It is necessary to trace both the reflected ray by the method just
described and the refracted ray by using Snell's Law, which
involves the the ray direction, optical density of the medium,
and
n. Then keep going with each of the two rays. The
refracted ray inside the medium might hit the surface again at an
angle that produces total internal reflection, or it might be
partly reflected and partly refracted again and then go on to hit
other objects, and so on--all this to find the brightness of one
pixel!
- If the surfaces are described parametrically instead of being
easy objects like spheres defined by relational equations
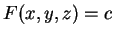 ,
then finding where the ray hits the surface can be much harder.
,
then finding where the ray hits the surface can be much harder.
- If the lighting source is at a finite point, the method is the
same except that
s will depend on
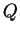 . You may wish also to
include a factor for the fact that brightness of a light source is
inversely proportional to the square of the distance it is away.
. You may wish also to
include a factor for the fact that brightness of a light source is
inversely proportional to the square of the distance it is away.
- The methods described so far produce strong shadows. Often an
ambient light source is added as well, meaning a light source that
illuminates all objects uniformly, with no particular direction, the
way light bouncing off white walls might. (``Ambient'' means ``surrounding''.
In calculus you may have seen Newton's law of cooling, which can be
described as telling how the temperature of a hot object approaches the
``ambient temperature'', meaning the air temperature of the surrounding room.)
- If the light source is in color, then you can consider its red,
green, and blue components separately and treat each as if they were
monochrome.
- The Phong formula can also include any additional constant
factors you want, say representing the fact that a diffusely reflecting
surface may not be fully reflective. (Some surfaces could be darker
than others.)
- If an object has color, in the Phong formula you can introduce
an extra factor that depends on color (red, green, or blue) and
expresses the property that some colors are reflected more than others.
- Phong's original formula allows a power of
n
 s,
say
s,
say
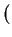 n
n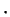 s
s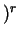 , where
, where 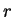 is a constant
is a constant 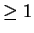 .
Because
n
.
Because
n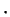 s is between 0 and 1, a higher power has the
effect of a sharper falloff of brightness for normal directions not
pointing near the light source.
s is between 0 and 1, a higher power has the
effect of a sharper falloff of brightness for normal directions not
pointing near the light source.
- Some books use a setup with the
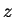 coordinate axis running the
other way, so that the viewpoint is on the negative
coordinate axis running the
other way, so that the viewpoint is on the negative 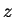 axis. Such
a coordinate system is left-handed, but the math is the same idea as
described in §
axis. Such
a coordinate system is left-handed, but the math is the same idea as
described in §![[*]](/lib/latex2html-icons/crossref.gif) . Another possibility is to put the
viewpoint at the origin and the viewplane at
. Another possibility is to put the
viewpoint at the origin and the viewplane at 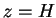 ; in this
case the ray from the viewpoint to
; in this
case the ray from the viewpoint to 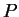 has the easy equation
x
has the easy equation
x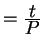 .
.



Next: ii_ray_tr
Up: ii_ray_tr
Previous: ii_ray_tr
Kirby A. Baker
2002-03-07