1. Inventing Surfaces

It is possible to invent surfaces of your own if you make them step-by-step. It helps especially to sweep them out by motions.

Example 1, revisited. To make a sphere of radius 1, first take an easy point, such as $(1,0,0)$. Make it into a vertical semicircle by applying $R _ t ^ {x\rightarrow z}$, where $t$ varies from $-\frac \pi 2$ to $\frac \pi 2$; you get $(1,0,0) R _ t ^ {x\rightarrow z}$. Then twist the semicircle around the $z$-axis by applying $R _ u ^ {x\rightarrow y}$, where $u$ varies from 0 to $2 \pi$. You get

P$(t,u) = (1,0,0) R _ t ^ {x\rightarrow z} R _ u ^ {x\rightarrow y}$, which reduces to

P$(t,u) = (\cos t \cos u, \cos t \sin u, \sin t)$ for $-\frac {\pi}2 \leq t \leq \frac {\pi}2, 0 \leq u \leq 2 \pi$.

Example 3, revisited. Pick an axis along which to twist the ribbon, say the $y$-axis. Imagine the ribbon as swept out by a moving line segment, as the time $t$ changes. Pick a line segment for time 0, say a segment of length 2 along the $z$-axis: $(0,0,u)$ for $-1 \leq u \leq 1$. At time $t$, the segment should be rotated by $R _ t ^ {x\rightarrow z}$ and translated along the $y$-axis a distance $t$ (a distance proportional to $t$ would also do), by adding $(0,t,0)$. The time interval is arbitrary, but $- \pi \leq t \leq \pi$ is nice, since it corresponds to one full twist. You get

P$(t,u) = (0,0,u) R _ t ^ {x\rightarrow z} + (0,t,0)$, which reduces to

P$(t,u) = ( -u \sin t, t, u \cos t)$, for $-\pi \leq t \leq \pi, -1 \leq u \leq 1$.

Example 4. Any graph $(f(t,u),g(t,u),h(t,u))$. In fact, this is the most general parametric surface. You might think you would get an interesting surface by just choosing $f,g,h$ to be unrelated messy functions, but such a method often gives disappointing results.

Example 5. A curve rotated about the $x$-axis, with radius some function $r(x)$, $a \leq x \leq b$:

The curve drawn in the $x,z$-plane would be $z = r(x)$. To make this parametric in one variable, use $x = t, y = 0, z = r(t)$, so that the points are $(t, 0, r(t))$. Now rotate about the $x$-axis by multiplying by $R _ u ^ {y\rightarrow z}$, for $0 \leq u \leq 2 \pi$. You get

P$(t,u) = (t, 0, r(t)) R _ u ^ {y\rightarrow z}$ = $(t, - r(t) \sin u, r(t) \cos u)$ for $a \leq t \leq b$, $0 \leq u \leq 2 \pi$.

Example 6. A torus (doughnut): Pick a small radius $r$ and a large radius $s$, say 1 and 3. Start with one point, $(r,0,0)$. Rotate it in the $x,z$-plane by $R _ t ^ {x\rightarrow z}$, to sweep out a circle. Then move the circle by a translation along the $x$-axis so that its center is moved to $(s,0,0)$. Then sweep out the surface by rotating around a vertical axis, using $R _ u ^ {x\rightarrow y}$ for $0 \leq u \leq 2 \pi$. You get

P$(t,u) = \left ( (r,0,0) R _ t ^ {x\rightarrow z} + (s,0,0) \right ) R _ u ^ {x\rightarrow y}$, which you can simplify, or program as is. (Be careful about parentheses in this formula. Which mathematical parentheses indicate a list of three coordinates and which are for grouping?)

Example 7. A Möbius strip: This is something like a combination of Examples 3 and 6. You need to move a line segment around a circle with time, turning it as you go. Start with a vertical line segment $(0,0,u)$, $-1 \leq u \leq 1$. Choose a radius $R > 1$. At time $t$, the segment should be rotated in the $x,z$-plane, translated by $(R,0,0)$, and then rotated by $R _ t ^ {x\rightarrow y}$, where $0 \leq t \leq 2 \pi$. But how fast should the segment be rotated in the $x,z$-plane? It should get a half-twist during the time it sweeps around the circle of radius $R$, so that the rotation should be $R _ {t/2} ^ {x\rightarrow z}$. You get

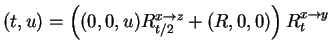P$(t,u) = \left ( (0,0,u) R _ {t/2} ^ {x\rightarrow z} + (R,0,0) \right ) R _ t ^ {x\rightarrow y}$ which you can simplify, or program as is. (Be careful about parentheses in this formula, lists versus grouping.)