5. Special matrices

(i)

The $n \times n$ identity matrix $I = \left [\begin{array}{cccc} 1&&&\\ &\cdot&&\\ &&\cdot&\\ &&&1 \end{array} \right ]$ (other entries 0)

(ii)

The $m \times n$ zero matrix O (all entries 0)

(iii)

scalar matrices $\left [\begin{array}{cccc} r&&&\\ &\cdot&&\\ &&\cdot&\\ &&&r \end{array} \right ] = rI$

(iv)

diagonal matrices in general, $\left [\begin{array}{cccc} d _ 1&&&\\ &\cdot&&\\ &&\cdot&\\ &&&d _ n \end{array} \right ]$

(v)

rotation matrices, representing a rigid motion that preserves orientation;

(vi)

reflection matrices, whose corresponding transformation gives a reflection in some ``mirror'' through the origin. In R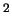$^ 2$, the mirror will be a line, and in R$^ 3$, the mirror will be a plane.

(vii)

shear matrices, by which we'll mean matrices that are the same as $I$ except that in some row one or more nondiagonal entries can be nonzero. Example: $\left [\begin{array}{cc} 1&3\\ 0&1 \end{array} \right ]$.