6. Signed angles between vectors in the plane--a practical guide

In R$^3$, given two vectors v, w at the origin, in talking about the angle $\theta$ between them you might as well allow only values $0 \leq \theta \leq \pi$, because the same angle can look clockwise or counterclockwise when seen from different directions. To find $\theta$, it's enough to use the dot product, which works in R$^n$ for any $n$. As in Section 3 above:

(1) $\cos \theta = {\frac {\mbox{\bf v} \cdot \mbox{\bf w}} {\vert \mbox{\bf v} \vert \vert \mbox{\bf w} \vert}}$.

In R$^2$, though, it makes sense to ask for $\theta$ with a sign. $\theta > 0$ means a counterclockwise angle and $\theta < 0$ means a clockwise angle. Possible values would be $-\pi < \theta \leq \pi$. This time dot products alone are not enough, because with cosines you can't tell the difference between $\theta$ and $-\theta$; for example, $\cos (-30 ^\circ) = \cos {30}^\circ$.

You might at first consider using $\sin \theta$ instead. In fact, there is a corresponding formula, as noted in section 5 above:

(2) $\sin \theta = D($v$,$w$) /{\vert \mbox{\bf v} \vert \vert \mbox{\bf w} \vert}$, where $D($v$,$   w$) = \det \left [\begin{array}{cc} v _ 1& v _ 2\\ w _ 1& w _ 2 \end{array} \right ]$.

However, with sines you can't tell the difference between $\theta$ and $\pi - \theta$; for example, $\sin 30 ^\circ = \sin 150 ^\circ$.

What about the tangent function? From (1) and (2) we would get

(3) $\tan \theta = {\frac{\displaystyle \sin \theta}{\displaystyle \cos \theta}} = ... ...e D(\mbox{\bf v},\mbox{\bf w})}{\displaystyle \mbox{\bf v} \cdot \mbox{\bf w}}}$,

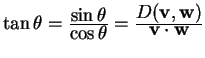where the denominators have been canceled. But the tangent has a similar problem: it can't distinguish between $\theta$ and $\theta + \pi$.

One way to get an exact $\theta$ would be to use two trig functions. Since you're solving for $\theta$ you would use two of the arc functions, which in C and C++ are acos( ), asin( ), and atan( ). The first would give you an angle in a specific range such as $0 \leq \theta \leq \pi$ for acos( ), and then you would use the second to change the angle if warranted (say, negating the angle if asin( ) is negative).

Fortunately, though, there is a single function in C and C++ that is designed expressly for this kind of application: the atan2(y,x) function. This function finds $\arctan \frac y x$ while paying attention to whether $x$ and $y$ are positive, negative, or zero; it returns a value between $-\pi$ and $\pi$, as desired. It works even if the denominator x is zero!

Thus in C or C++ (using subscripts 0,1 for 1,2), you can find $\theta$ by

(4) theta = atan2(v[0]*w[1]-v[1]*w[0], v[0]*w[0]+v[1]*w[1]);

There will be an error if both arguments are zero.

Note. In some versions of C and C++ this function may be built in; in others you may need to use #include<math.h> and to compile with a flag -lm. This kind of function is also available in other languages, but check which argument is for x and which for y.