Next: About this document ...
Up: q_fin_ann
Previous: q_fin_ann
Announcements for the Final Exam
Room change: The final exam room will be Geology 3656. That's
on the left side of the Chem complex.
The final exam will be Tuesday, June 15, 11:30-2:30.
Conditions:
120 points
Closed book.
Calculators permitted, except those that can do ``modular
arithmetic''
Format of exam:
Pretty much like the midterm, except that there will be
more 10-point problems and more shorter-answer problems.
No bluebooks needed.
Coverage:
All lectures and homework, including problems ``not to hand in''.
Text: All chapters in which reading and/or problems have been assigned.
In general: All topics mentioned in lectures and homework problems.
Emphasis: Topics from before the midterm are included but topics
after the midterm will be emphasized. Of course, some topics from
before the midterm, such as congruences, are part of later
topics anyway.
Comments on some topics:
- Be especially aware of some topics that stretched through
more than one homework assignment:
-
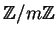 and its units
and its units
- Orders of units in rings and especially in fields
- Finite fields and especially generators of the nonzero elements
- Applications of finite fields, especially to Latin squares,
block designs, error-correcting codes, and cryptology.
- The Euler
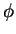 function.
function.
- The Chinese Remainder Theorem in various versions.
- Applications of linear algebra over finite fields,
especially
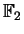 .
.
You don't need to be
able to quote straight linear algebra theorems, but
you do need the ideas of linear combinations, span,
subspaces, and dimension. Also, understand the idea
and applications of the fact that for fields
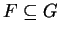 ,
, 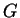 is a vector space over
is a vector space over 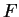 .
.
- For cryptology, know Diffie-Hellman and RSA. Know Rijndael to
the extent discussed at the beginning of handout L; you don't
need to memorize the algorithm itself.
- Any simultaneous-congruence problems will be for either (a)
coprime moduli and two or more congruences, or (b) moduli
not coprime and just two congruences.
- Theorems whose proofs you should know especially:
- Proof by induction, whether the trivial kind or not.
- The steps leading from division of integers to unique prime
factorization
- All versions of Fermat/Euler, including for units of a finite
ring. (See homework solutions.)
- Why the Euler
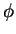 function has
function has
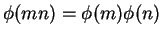 if
if 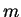 and
and 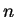 are coprime.
are coprime.
- Why the size of a finite field has to be a prime power.
- The fact that the nonzero elements of a finite field have a
generator (developed in a series of homework problems)
- The ``exponents dividing
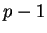 '' test for being the generator
of
'' test for being the generator
of
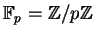
- For topics covered during the last three lectures, any problems
will stick closely to what you had in lecture and homework.
Review:
In class as part of lecture on Friday, June 11.
Office hours: Thursday, June 10, 11:00-12:00 and Monday, June 14,
11:00-12:00.



Next: About this document ...
Up: q_fin_ann
Previous: q_fin_ann
Kirby A. Baker
2004-06-09
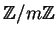 and its units
and its units
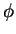 function.
function.
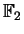 .
.
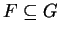 ,
, 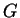 is a vector space over
is a vector space over 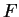 .
.
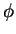 function has
function has
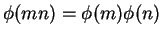 if
if 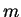 and
and 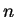 are coprime.
are coprime.
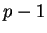 '' test for being the generator
of
'' test for being the generator
of