3. Bytes and algebra

As you know, a byte means 8 bits (binary digits), e.g., 10110110, or in hexadecimal for short, B6. In running the algorithm, bytes are interpreted in two different ways at different times:

1. A byte is a row vector of length 8 with entries in the field $\mathbb{F}_ 2$. From this point of view, if we add two bytes they are added bitwise mod 2, which in a computer is the ``exclusive or'' operation, a^b in C++.

2. A byte represents an element of the field $\mathbb{F}_ {2^8}$ with $2^8 = 256$ elements. In this interpretation, there is a particular element $\alpha$ in that field and powers of $\alpha$ form a basis of $\mathbb{F}_ {2^8}$ as an 8-dimensional vector space over the field $\mathbb{F}_ 2$ as coefficients. Each coefficient is one bit. Examples:
   • 10110110 means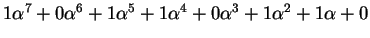 $1 \alpha^7 + 0 \alpha^6 + 1 \alpha^5 + 1 \alpha^4 + 0 \alpha^3 + 1 \alpha^2 + 1 \alpha + 0$, or simply $\alpha^7 + \alpha^5 + \alpha^4 + \alpha^2 + \alpha$.

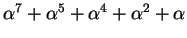   • 1 of the field is 00000001 (why?).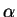

   • $\alpha$ itself is 00000010 (why?).

   The $\alpha$ chosen is a generator of the nonzero elements of the field with the property that $\alpha^8 = \alpha^4 + \alpha^3 + \alpha + 1$.

   Just as you can multiply any two complex numbers once you know that $i^2 = -1$ in $\mathbb{C}$, you can multiply any two expressions involving powers of $\alpha$ once you know the equation for $\alpha^8$.

   Example: What is 00010000 times itself? This is $\alpha^4$, so times itself we have $\alpha^8$, which can then be rewritten in terms of lower powers using the equation, yielding 00011011 as the answer.