Due Friday, April 23.
To do but not hand in:
p. 50 Ex. 3;
p. 52 Ex. 7, 13;
p. 65 Ex. 3;
p. 67 Ex 5;
p. 74 Ex. 5;
D-2. (Do be sure to try D-2 to see what it is saying.)
To hand in:
p. 49 Ex. 2;
p. 53 Ex. 18;
p. 55 Ex. 1;
p. 65 Ex. 5;
p. 67 Ex. 6;
p. 74 Ex. 6;
Ex. D-1.
Problem
D-1. There is a link on the Math 117 home page to an applet
that shows which entries in Pascal's triangle are divisible by
an integer that you specify. The integer is changed by clicking
on Divisor+ or Divisor-. The current integer is
shown at the bottom of your browser.
(a) Make the integer a prime ![]() , say
, say ![]() or
or ![]() . Which
colored dots correspond to the statement of Problem C-2(b)?
. Which
colored dots correspond to the statement of Problem C-2(b)?
(b) Explain why the colored dots in (a) are the top of a triangle. In other words, why are the dots in the triangle colored, and why aren't the dots just outside the triangle colored? (Don't forget the recursive description of binomial coefficients, and think in terms of congruences.)
(c) Below the triangle mentioned in (b) above there are more triangles
of the same size. Formulate a divisibility statement that describes
the top rows of these triangles. (In other words, state that
![]() divides certain binomial coefficients that depend on the
triangle in the row.)
divides certain binomial coefficients that depend on the
triangle in the row.)
(d) Invent some divisibility statement to describe the top
rows of the larger and larger triangles divisible by ![]() , just
the first one of each size.
, just
the first one of each size.
Problem
D-2. (a) Traditionally, ![]() means the number
of primes up to
means the number
of primes up to ![]() . For example,
. For example, ![]() (a hundred million)
is 5,761,455. What is
(a hundred million)
is 5,761,455. What is ![]() ?
?
Describing the distribution of prime numbers is a very
challenging problem. In one sense they seem randomly
distributed, but obviously they aren't random since a given
integer is either prime or not. The ``density'' of primes (the
proportion of integers that are prime) goes down as you look at
larger and larger numbers. Gauss (``gowss'', 1777-1855) observed that
apparently their density near ![]() is
is
![]() , in the
sense that if you look at a stretch of integers near
, in the
sense that if you look at a stretch of integers near ![]() about
that proportion of them are apt to be prime1.
about
that proportion of them are apt to be prime1.
(b) The attached sheet shows blocks of primes with various starting
values. Does the block starting with 1,000,000 have more primes or
fewer than Gauss' density observation predicts? How about the
block starting at ![]() ? (Primes this large are used in
encryption.)
? (Primes this large are used in
encryption.)
Because of his density observation, Gauss predicted that
for large ![]() ,
, ![]() should be close to
should be close to ![]() , the ``logarithmic
integral'', given by
, the ``logarithmic
integral'', given by
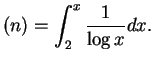
(c) For ![]() , how close to 1 is the ratio of
, how close to 1 is the ratio of ![]() to
to
![]() ?
?
(d) The Riemann Hypothesis (``ree-mahn'', 1826-1866), an unproven
conjecture with a million-dollar prize for its solution, states roughly
that the error
![]() Li
Li![]() has about half as many decimal
digits as
has about half as many decimal
digits as ![]() , or fewer than that, as
, or fewer than that, as
![]() . Does
this seem plausible for
. Does
this seem plausible for
![]() ? Here
? Here ![]() 279,238,341,033,925 and
Li
279,238,341,033,925 and
Li![]() 279,238,344,248,557. ...
(Notice that the error is an extremely small percentagewise.)
279,238,344,248,557. ...
(Notice that the error is an extremely small percentagewise.)