Due Monday, April 19.
Note: In this assignment, use induction (either version) whenever you think that's the best method of proof. But also be alert for opportunities to use direct proofs that avoid induction.
Problems from these pages do not have to be done unless assigned.
To do but not hand in:
p. 27, Ex. 6;
p. 29, Ex. 5;
p. 35, Ex. 15;
C-1, C-2, C-4, C-6, C-8 below.
To hand in:
p. 27, Ex. 11;
p. 35, Ex. 10;
C-3, C-7, C-9, C-10, C-12, C-13 below;
Problem
C-1. Recall that Stirling's approximate formula for ![]() is
is
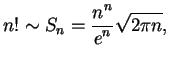
Using Stirling's approximation, find an approximation for
![]() .
.
Problem C-2. (a) Write out Pascal's Triangle through row 7.
(b) Notice that for each prime ![]() , all the coefficients in
row
, all the coefficients in
row ![]() are divisible by
are divisible by ![]() , except for the 1's at the
ends. In other words,
, except for the 1's at the
ends. In other words,
![]() for
for ![]() .
Prove that this is true for all primes
.
Prove that this is true for all primes ![]() . (Useful principle for primes:
. (Useful principle for primes:
![]()
![]() . Or think in terms of prime
factorizations.)
. Or think in terms of prime
factorizations.)
Problem C-3. (a) Develop and prove a simple formula for
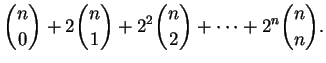
(b) Develop and prove a simple formula for
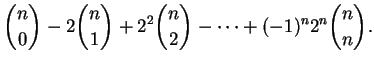
Problem C-4. In the ASCII computer code for characters, which is understood by essentially all computers, printers, etc., the upper-case letters A, B, C,...have codes 65, 66, 67, etc. (in the decimal version) and the lower-case letters have decimal codes 97, 98, 99, etc. Explain how these codes make more sense in binary (which is what the computer actually uses).
Problem
C-5. (a) Describe ![]() in binary.
in binary.
(b) Describe ![]() in hexadecimal if
in hexadecimal if ![]() is divisible by 4.
is divisible by 4.
Problem
C-6. (a) What is ![]() , approximately, as a power of 10?
, approximately, as a power of 10?
(b) If you buy a computer whose hard disk has 80 gigabytes, which we can think of as numbered locations, how many bits (binary digits) does it take to express the location numbers? How many hexadecimal digits? (One byte is 8 bits, but that doesn't matter here since it's the bytes that are numbered.)
Problem
C-7. (a) Find the square of
![]() by using a hand
calculator and ``superdigits'' base
by using a hand
calculator and ``superdigits'' base ![]() . Your work will have
the pattern shown. (This has more lines than the multiplication
algorithm we learned in elementary school, in which some lines are
combined by carrying. Here carrying occurs only in the final addition.)
. Your work will have
the pattern shown. (This has more lines than the multiplication
algorithm we learned in elementary school, in which some lines are
combined by carrying. Here carrying occurs only in the final addition.)
| D | D | |||
| D | D | |||
| D | D | |||
| D | D | |||
| D | D | |||
| D | D | |||
| D | D | D | D |
(b) In binary, do a long division of ![]() into
into ![]() (getting
a quotient and remainder). Check by using decimal.
(getting
a quotient and remainder). Check by using decimal.
Problem C-8. Which positive integer less than 1000 has the most divisors? (Reasoning?)
Problem C-9. There is a row of 100 empty lockers, all shut. A student comes by and opens every locker. Another student comes by and closes lockers 2, 4, 6, and so on. Another student comes by and changes lockers 3, 6, 9, and so on, opening closed ones and closing open ones. Another student comes by and changes lockers 4, 8, 12, and so on. This process continues up to 100 students. At the end, which lockers are open, and why?
Problem
C-10. Find
![]() two ways: (a) By the Euclidean algorithm;
(b) by factoring. (For the Euclidean algorithm, you can use a calculator;
for factoring, you may use the calculator on the class web page.)
two ways: (a) By the Euclidean algorithm;
(b) by factoring. (For the Euclidean algorithm, you can use a calculator;
for factoring, you may use the calculator on the class web page.)
Problem C-11. Find two integers among 1 to 100 such that the Euclidean algorithm takes as many steps as possible. (Give your reasoning.)
Problem
C-12. The Fibonacci sequence is
![]() ,
where each term is the sum of the preceding two. In other words, if
we call these terms
,
where each term is the sum of the preceding two. In other words, if
we call these terms
![]() , the sequence
is defined by
, the sequence
is defined by ![]() ,
, ![]() , and recursively
, and recursively
![]() for
for ![]() .
.
(a) Show that every two consecutive terms of the Fibonacci sequence are relatively prime (i.e., have gcd = 1).
(b) Develop and prove a simple formula for the value of
![]() . (Combine the cases of
. (Combine the cases of ![]() even and
even and ![]() odd if you can.)
odd if you can.)
(c) How does Bezout's Theorem work for consecutive terms of the Fibonacci
sequence? (Can you say explicitly what the coefficients ![]() and
and ![]() are?)
are?)
(d) Prove that
![$ \left[\begin{array}{cc}F _ {n-1}& F _ n\ F _ n& F _ {n+1}\end{array}\right]
= \left[\begin{array}{cc}0&1\ 1&1\end{array}\right] ^ n$](img35.gif) . This is valid even for
. This is valid even for ![]() if we
let
if we
let
![]() (which fits the recursive definition for the
Fibonacci sequence).
(which fits the recursive definition for the
Fibonacci sequence).
(e) Does (c) help with solutions for any other part of the problem?
Problem
C-13. (a) The golden mean or golden ratio is the positive number
![]() such that
such that
![]() . Find
. Find ![]() explicitly using
the quadratic formula.
explicitly using
the quadratic formula.
(b) Verify that the other solution of
![]() is
is
![]() . (Note:
. (Note:
![]() and so
and so
![]() .)
.)
(c) Show that the sequence
![]() follows the same
recursion as the Fibonacci sequence. What about
follows the same
recursion as the Fibonacci sequence. What about
![]() ?
?
(d) A direct formula for Fibonacci: Show that
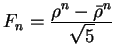 .
.
(Note: Since
![]() , as
, as ![]() gets large the term involving
gets large the term involving
![]() becomes negligible. In fact, even for small
becomes negligible. In fact, even for small ![]() ,
,
![]() can be obtained by rounding
can be obtained by rounding
![]() to the nearest integer. For example,
to the nearest integer. For example,
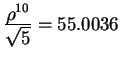 and
and
![]() .)
.)
Problem C-14. In computer graphics, a Bézier1curve is a parametric curve with polynomial coefficient functions, specified not by giving the polynomial coefficients but rather by giving ``control points''. Binomial coefficients are needed in the construction.
(a) Starting from the class home page
http://www.math.ucla.edu/~baker/117/ try the Bézier
demo, following the directions for it. Move the control points
around a lot to get a feel for the possibilities. Can you make
a curve that loops around to cross itself?
(Note: These are cubic (degree 3) Bézier curves, which are the most common. As you see, we don't use the whole infinite curve but just a segment.)
Bézier curves are constructed as follows (for degree 3):
Step 1: Expand
![]() , as
in the binomial theorem.
, as
in the binomial theorem.
Step 2: Put these terms in a list instead of adding them:
![]() .
.
Step 3: Put ![]() , to get cubic polynomials, which we
can call
, to get cubic polynomials, which we
can call
![]() .
.
Step 4: If the four control points are
![]() ,
the curve is
,
the curve is
![]() ,
for
,
for
![]() , where we treat points like vectors.
, where we treat points like vectors.
Here recall that a parametric plane curve can be thought of
as a moving point
![]() , where
, where ![]() is time.
For example, if the control points are
is time.
For example, if the control points are
![]() then
then
![]() ,
,
or looking at coordinates separately,
![]() and
and
![]() .
.
(b) For control points ![]() , what are
, what are ![]() and
and ![]() ?
?
(c) Show that the coefficients add to 1 at all times. (So we're really taking a ``weighted average'' of the four control points, with total weight 1. The weights change with time, and that makes the point move to trace out the curve.)