Here is a review of the ``exchange'' proof that two finite bases of a vector space must have the same size.
This proof is important because it can be done directly from the basic definition of a vector space instead of requiring facts about matrices.
If you are asked to do this proof, it is Lemma 2 that is expected.
Let ![]() be a vector space.
be a vector space.
Lemma 1. If
![]() are linearly dependent,
then some
are linearly dependent,
then some ![]() is in the span of the preceding vectors
is in the span of the preceding vectors
![]() .
.
Proof. If
![]() 0,
with
0,
with
![]() not all 0, let
not all 0, let ![]() be
the highest index with
be
the highest index with
![]() . Then
. Then
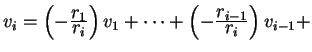 0
0![]() 0.
0.
Remark. This was simple, but in the theory of vector spaces
this is where we need the the field property that every nonzero
field element has a multiplicative inverse. If we tried to use
![]() for scalars, Lemma 1 would fail.
for scalars, Lemma 1 would fail.
Corollary. [not needed for the proof of the theorem] If none of
![]() is in the span of the preceding vectors,
then this list is linearly independent
is in the span of the preceding vectors,
then this list is linearly independent
Proof. This is just the contrapositive of the statement of Lemma 1.
Note. To say that ![]() is not in the span of the
preceding vectors means that
is not in the span of the
preceding vectors means that
![]() 0, because the
span of no vectors is
0, because the
span of no vectors is
![]() 0
0![]() .
.
Lemma 2. If ![]() is spanned by
is spanned by
![]() and
if
and
if
![]() are linearly independent in
are linearly independent in ![]() , then
, then
![]() .
.
Proof. We keep making new spanning sets by ``exchanging''
![]() for
for
![]() one vector at a time, as follows.
one vector at a time, as follows.
Start with
![]() ,
,
which span ![]() . Now consider the list
. Now consider the list
![]() .
.
Since
![]() span
span![]() this new list
is linearly dependent. By Lemma 1, some vector is in the span
of the preceding vectors. It can't be
this new list
is linearly dependent. By Lemma 1, some vector is in the span
of the preceding vectors. It can't be ![]() since
since
![]() 0 (being in a linearly independent set of vectors). So
it is
0 (being in a linearly independent set of vectors). So
it is ![]() for some
for some ![]() , say
, say ![]() . Then we can
remove
. Then we can
remove ![]() from the list and still have a spanning
set:
from the list and still have a spanning
set:
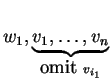 .
.
Now consider the list
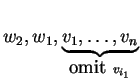 .
.
Again, since ![]() was in the span of the preceding list,
the new list is linearly dependent and some vector is in the
span of the preceding. Again, it can't be
was in the span of the preceding list,
the new list is linearly dependent and some vector is in the
span of the preceding. Again, it can't be ![]() or
or ![]() because
because
![]() are linearly independent.
Therefore we can remove another vector
are linearly independent.
Therefore we can remove another vector ![]() from the
list and still have a spanning set:
from the
list and still have a spanning set:
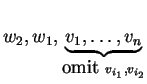 .
.
We continue in this way, putting in ![]() 's at the left and taking
out
's at the left and taking
out ![]() 's. If
's. If ![]() then we will run out of
then we will run out of ![]() 's and
have a spanning set consisting of some but not all of
's and
have a spanning set consisting of some but not all of
![]() , which is impossible because no
, which is impossible because no ![]() is
in the span of the rest. This is a contradiction, so
is
in the span of the rest. This is a contradiction, so ![]() .
.
Remarks. (1) It might be neater to throw in ![]() first
instead of
first
instead of ![]() , then
, then ![]() , etc., so
, etc., so
![]() appear in the original order.
appear in the original order.
(2) This is really an informal proof by induction. We may discuss proof by induction later.
(3) Notation for this proof is a special problem. In describing
the list of
![]() with
with ![]() omitted,
we would usually say
omitted,
we would usually say
![]() . That's fine, but for omitting two vectors it doesn't
work because we don't know which of
. That's fine, but for omitting two vectors it doesn't
work because we don't know which of ![]() ,
, ![]() occurs first.
occurs first.
Still another approach is to say after each step that since the list
still spans in any order, by re-indexing we can assume that it's
![]() that is to be deleted, then
that is to be deleted, then ![]() , etc. That's
actually a neater way to say it, but re-indexing after every step
seems harder to think about.
, etc. That's
actually a neater way to say it, but re-indexing after every step
seems harder to think about.
Theorem. (``invariance of dimension'') If ![]() has a basis
of
has a basis
of ![]() elements and a basis of
elements and a basis of ![]() elements, then
elements, then ![]() .
.
Proof. Since a basis is both linearly independent and a spanning set,
Lemma 2 applies both ways around to show ![]() and
and ![]() .
Therefore
.
Therefore ![]() .
.
Definition. If ![]() has a basis of
has a basis of ![]() elements then we say
elements then we say
![]() has dimension
has dimension ![]() .
.
The Theorem tells us that this definition is not ambiguous; there is only one possible dimension.