p. 73, Ex. 4.
Yes, there is such a linear transformation: The
two vectors
![]() and
and
![]() are
not scalar multiples of each other and so are linearly
independent. Therefore they can be extended to a basis
are
not scalar multiples of each other and so are linearly
independent. Therefore they can be extended to a basis
![]() of
of
![]() . By Theorem 1, given any
three vectors
. By Theorem 1, given any
three vectors
![]() in a second vector
space, which can be
in a second vector
space, which can be
![]() , there is a linear transformation
taking
, there is a linear transformation
taking
![]() for each
for each ![]() . We can choose
. We can choose
![]() ,
,
![]() and
and ![]() anything we want, say
anything we want, say ![]() .
.
In this problem we were not actually asked to find the transformation.
p. 73, ex. 5.
Notice that
![]() .
Since a linear transformation preserves linear relations, if
such a
.
Since a linear transformation preserves linear relations, if
such a ![]() exists then we should have
exists then we should have
![]() also. But instead,
also. But instead,
![]() . Therefore such a linear transformation
does not exist.
. Therefore such a linear transformation
does not exist.
p. 73, Ex. 6.
By
![]() the authors mean our standard basis vector
the authors mean our standard basis vector
![]() . We know
. We know
![]() for
for
![$ A =
\left[\begin{array}{cc}a&c\\ b&d\end{array}\right]$](img20.gif) . To display the answer in a form like
Example 1, calculate
. To display the answer in a form like
Example 1, calculate
![$ \left[\begin{array}{cc}a&c\\ b&d\end{array}\right] \left[\begin{array}{c}x\\ y\end{array}\right] =
\left[\begin{array}{cc}ax+cy\\ bx+dy\end{array}\right]$](img21.gif) , which says
, which says
![]() .
.
p. 73, Ex. 8.
This is a transformation on
![]() , so
we can use
, so
we can use ![]() where
where ![]() is a
is a
![]() matrix.
The range of
matrix.
The range of ![]() is the column space of
is the column space of ![]() , so take
, so take
![]() to have columns
to have columns
![$ \left[\begin{array}{r}1\\ 0\\ -1\end{array}\right]$](img27.gif) and
and
![$ \left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$](img28.gif) .
For the third column of
.
For the third column of ![]() we can take any vector already in
the span of those two columns, say
we can take any vector already in
the span of those two columns, say
![$ \left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$](img29.gif) . So we
can choose
. So we
can choose
![$ A = \left[\begin{array}{rrr}1&1&0\\ 0&2&0\\ -1&2&0\end{array}\right]$](img30.gif) .
.
For Problem O-1:
Advice: First write down some examples of functions
![]() . You will see that you need a list of
three numbers for each, so each function corresponds to a
triple. Furthermore, functions add pointwise and triples
coordinatewise, so that vector addition is compatible with the
correspondence, and similarly for multiplication by scalars.
That gives the following idea.
. You will see that you need a list of
three numbers for each, so each function corresponds to a
triple. Furthermore, functions add pointwise and triples
coordinatewise, so that vector addition is compatible with the
correspondence, and similarly for multiplication by scalars.
That gives the following idea.
Given
![]() , define
, define
![]() . Then
. Then
![]() Functions
Functions![]() is one-to-one and onto. Also,
is one-to-one and onto. Also, ![]() is a linear
transformation, because the pointwise operations on functions
correspond to the coordinatewise operations on
is a linear
transformation, because the pointwise operations on functions
correspond to the coordinatewise operations on ![]() -tuples.
-tuples.
The importance of this problem is the perspective that it gives:
Our first examples of vector spaces included some consisting of
![]() -tuples and some consisting of functions. Now it is
becoming apparent that even the
-tuples and some consisting of functions. Now it is
becoming apparent that even the ![]() -tuples were really made of
functions in disguise. How about examples such as
Mat
-tuples were really made of
functions in disguise. How about examples such as
Mat![]() ? This could be viewed as
Functions
? This could be viewed as
Functions![]() , where
, where
![]() is the set
is the set
![]() of
pairs of indices, or more simply,
of
pairs of indices, or more simply,
![]() .
.
For Problem O-2:
(b) Just make sure that both of ![]() and
and ![]() are on
the same line. One of them could be the zero vector.
are on
the same line. One of them could be the zero vector.
A shear is a transformation that moves points parallel to some
line. The line is the ![]() -axis in the case of this program.
-axis in the case of this program.
For Problem O-3:
(a) Yes: For closure under addition,, suppose
![]() . We must show that
. We must show that
![]() .
To say
.
To say
![]() is the same as saying that
is the same as saying that
![]() for some
for some
![]() (
(![]() ). Since
). Since
![]() is a subspace,
is a subspace,
![]() , and since
, and since
![]() preserves addition,
preserves addition, ![]() contains
contains
![]() . For closure
under multiplication by scalars ...[continue with similar
proof].
. For closure
under multiplication by scalars ...[continue with similar
proof].
(b) Yes: For closure under addition, suppose
![]() , which is the same as saying that
, which is the same as saying that
![]() . We must show that
. We must show that
![]() ,
which is the same as saying that
,
which is the same as saying that
![]() .
Since
.
Since ![]() is linear,
is linear,
![]() ,
which is in
,
which is in ![]() because
because ![]() is closed under addition.
Therefore
is closed under addition.
Therefore
![]() as required. For
closure under multiplication by scalars ...[continue with
similar proof].
as required. For
closure under multiplication by scalars ...[continue with
similar proof].
For Problem O-4:
(ii) is false, while (i), (iii), (iv) are true. (iv) is proved in the handout.
For (i):
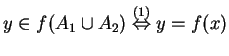 for
some
for
some
![]()
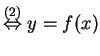 for some
for some ![]() with
with
![]() or
or
![]()
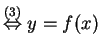 for some
for some
![]() or some
or some
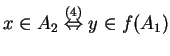 or
or
 , where the
reasons for the double implications are (1) definition of
, where the
reasons for the double implications are (1) definition of
![]() subset
subset![]() , (2) definition of
, (2) definition of ![]() , (3) the way ``for
some'' (really
, (3) the way ``for
some'' (really ![]() ) interacts with ``or'', (4) definition of
) interacts with ``or'', (4) definition of
![]() subset
subset![]() , (5) definition of
, (5) definition of ![]() . Therefore
. Therefore
![]() ,
,
For (ii):
The clearest kind of example is one where
![]() but
but
![]() is not empty. For
instance let
is not empty. For
instance let
![]() , let
, let ![]() , define
, define
![]() by
by
![]() , let
, let
![]() ,
and let
,
and let
![]() . Then
. Then
![]() but
but
![]() .
.
For (iii):
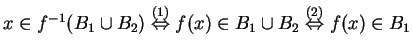 or
or 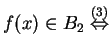
![]() or
or  ,
,
where the reasons for the double implications are (1) definition
of ![]() , (2) definition of
, (2) definition of ![]() , (3) definition of
, (3) definition of ![]() ,
(4) definition of
,
(4) definition of ![]() . Therefore
. Therefore
![]() .
.