


Next: About this document ...
Up: s_inv
Previous: s_inv
Nonsingular matrices and transformations
This concerns square matrices and also transformations
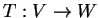 where
where 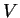 and
and 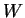 have the same finite dimension.
have the same finite dimension.
Theorem. Let 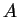 be an
be an
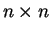 matrix with entries
in a field
matrix with entries
in a field 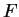 , with the corresponding matrix transformation
, with the corresponding matrix transformation
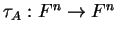 . Also let
. Also let
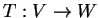 be a
linear transformation between vector spaces over
be a
linear transformation between vector spaces over 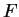 , both
of dimension
, both
of dimension 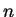 , such that
, such that 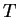 has matrix
has matrix 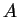 with
respect to particular bases of
with
respect to particular bases of 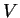 and
and 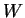 . The following
conditions are equivalent.
. The following
conditions are equivalent.
-
det
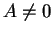 .
.
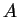 row-reduces to the
row-reduces to the
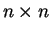 identity matrix.
identity matrix.
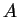 has rank
has rank 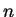 (``full rank'', meaning the maximum rank possible).
(``full rank'', meaning the maximum rank possible).
- The rows of
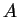 are linearly independent.
are linearly independent.
- The columns of
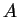 are linearly independent.
are linearly independent.
- Some system of linear equations with coefficient matrix
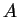 has a
unique solution.
has a
unique solution.
- Every system of linear equations with coefficient matrix
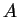 has a
unique solution.
has a
unique solution.
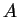 has a right inverse, i.e., there is an
has a right inverse, i.e., there is an
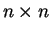 matrix
matrix
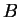 with
with 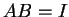 .
.
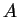 has a left inverse, i.e., there is an
has a left inverse, i.e., there is an
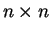 matrix
matrix
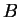 with
with 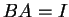 .
.
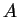 has a two-sided inverse
has a two-sided inverse 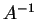 .
.
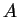 has nullity 0; in other words,
nullspace
has nullity 0; in other words,
nullspace 0
0 .
.
-
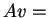 0
0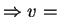 0
0
- 0 is not an eigenvalue of
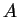 , i.e., there is no
, i.e., there is no 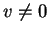 with
with
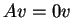 .
.
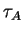 is one-to-one.
is one-to-one.
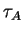 is onto.
is onto.
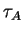 is an isomorphism of
is an isomorphism of 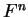 with itself
(an ``automorphism'' of
with itself
(an ``automorphism'' of 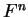 )
)
-
Nullspace
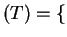 0
0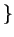 .
.
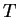 is one-to-one.
is one-to-one.
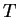 is onto.
is onto.
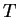 is an isomorphism.
is an isomorphism.
- The matrix of
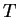 with respect to any bases of
with respect to any bases of 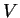 and
and
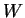 is nonsingular.
is nonsingular.
Definition. When any (and so all) of these conditions is
satisfied, then 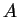 is said to be nonsingular. Otherwise A
is singular.
is said to be nonsingular. Otherwise A
is singular.
(``Singular'' means ``special'' or ``unusual'', not to be confused with
``single''. So a system of linear equations with nonsingular
coefficient matrix has a single solution.)



Next: About this document ...
Up: s_inv
Previous: s_inv
Kirby A. Baker
2001-11-07
![]() where
where ![]() and
and ![]() have the same finite dimension.
have the same finite dimension.
![]() be an
be an
![]() matrix with entries
in a field
matrix with entries
in a field ![]() , with the corresponding matrix transformation
, with the corresponding matrix transformation
![]() . Also let
. Also let
![]() be a
linear transformation between vector spaces over
be a
linear transformation between vector spaces over ![]() , both
of dimension
, both
of dimension ![]() , such that
, such that ![]() has matrix
has matrix ![]() with
respect to particular bases of
with
respect to particular bases of ![]() and
and ![]() . The following
conditions are equivalent.
. The following
conditions are equivalent.
![]() is said to be nonsingular. Otherwise A
is singular.
is said to be nonsingular. Otherwise A
is singular.