Assignment #5

Quiz 5 in discussion section, Tuesday, October 30: One of these two simple problems: (a) Show that a linear transformation is uniquely determined by its values on a basis. (b) For a linear transformation $T$, show that $T(v _ 1) = T(v _ 2) \Leftrightarrow (v _ 1 - v _ 2) \in$   NullSpace$(T)$.

Assignment due in lecture Wednesday, October 31 (shorter because of the midterm)

where	Do but don't hand in	Hand in
p. 73	Ex's 4, 5, 6, 8
O		O-1, O-2, O-3, O-4

(For Ex. 4, see Theorem 1.)

Problem O-1. Recall that for a set $S$ and field $F$, Functions$(S\rightarrow F)$ is a vector space when vector-space operations are defined pointwise.

Show that if $S = \{1,\ldots, n\}$, then $F^n \cong$   Functions$(S\rightarrow F)$. (Therefore any finite-dimensional vector space over a field $F$, being isomorphic to $F^n$ for some $n$, is isomorphic to a vector space of functions.)

Problem O-2. Log onto a computer and run Netscape or Internet Explorer. You are welcome to use the PIC Lab, BH 2817. If any of the following doesn't work, let me know.

On the class home page, click on ``Linear transformation demo in Java''. After the page loads, click on ``Linear program''. You should see the domain and image of a linear transformation on $\mathbb{R}^2 \rightarrow \mathbb{R}^2$. Then click on the button with a house to select that picture in the domain. You should find that you can drag the vectors on the right that are images of $e _ 1$ and $e _ 2$. The matrix entries shown will change as you do.

Try each of the following and write down the corresponding matrix:

(a) Invent a transformation that distorts the house.

(b) Invent a transformation that takes the whole house into a single line (a singular transformation).

(c) through (i): At the upper right, select different kinds of transformations. For each, if there is any choice in the example, invent an example that is different from the default example. Otherwise, copy down the default example.

Problem O-3. Let $X$ and $Y$ be sets and let $f:X\rightarrow Y$ be a function. (People also say ``map'' or ``mapping''). By the definition of a function, each element $x \in X$ has a unique image $f(x) \in Y$.

There is also a simple notation for how $f$ treats subsets: If $A$ is any subset of $X$, then $f(A)$ is a shorthand for the set of all images of elements in $A$; in symbols, $f(A) = \{f(x)\vert x \in A\}$. For example, if $f:\mathbb{R}\rightarrow \mathbb{R}$ is given by $f(x) = x^2$, then $f([0,2]) = [0,4]$.

In the other direction, if $B$ is any subset of $Y$, then $f^{-1}(B)$ is a shorthand for the set of all elements of $X$ that map into $B$; in symbols, $f^{-1}(B) = \{x \in A\vert f(x) \in B\}$. For example, if $f:\mathbb{R}\rightarrow \mathbb{R}$ is given by $f(x) = x^2$, then $f^{-1}([0,4]) = [-2,2]$.

For a single element $y \in Y$, people often write $f^{-1}(y)$ when they mean $f^{-1}(\{y\})$, but $f^{-1}(y)$ is definitely a subset since it could have more than one element or it could be empty. For example, if $f:\mathbb{R}\rightarrow \mathbb{R}$ is given by $f(x) = x^2$, then $f^{-1}(\{9\}) = \{-3,3\}$, and $f^{-1}(\{-1\}) = \emptyset$. But if $f$ is a one-to-one correspondence then $f^{-1}$ is a function.

Let $T:V\rightarrow W$ be a linear transformation between vector spaces.

(a) If $S$ is a subspace of $V$, is $T(S)$ necessarily a subspace of $W$?

(b) If $U$ is a subspace of $W$, is $T^{-1}(U)$ necessarily a subspace of $V$?

(Give reasoning.)

Problem O-4. Here are four possible rules about mapping subsets. Three are true and one is false. Identify which is false, prove the first two true ones, and find a counterexample for the false one.

$$\begin{array}{crrcl} ?&\mbox{(i)} &f(A _ 1 \cup A _ 2) &=& f... ...1 \cap B _ 2) &=& f^{-1}(B _ 1) \cap f^{-1}(B _ 2). \end{array}$$

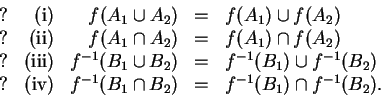
Sample: (iv) is true. To prove it, since both sides are sets we show they are equal by showing they have the same elements:

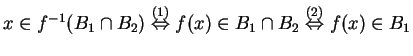$x \in f^{-1}(B _ 1 \cap B _ 2) \stackrel{(1)}{\Leftrightarrow} f(x) \in B _ 1 \cap B _ 2 \stackrel{(2)}{\Leftrightarrow} f(x) \in B _ 1$    and $f(x) \in B _ 2 \stackrel{(3)}{\Leftrightarrow}$
$x \in f^{-1}(B _ 1)$    and $x \in f^{-1}(B _ 2) \stackrel{(4)}{\Leftrightarrow} x \in f^{-1}(B _ 1) \cap f^{-1}(B _ 2)$,

where the reasons for the double implications are (1) definition of $f^{-1}$, (2) definition of $\cap$, (3) definition of $f^{-1}$, (4) definition of $\cap$.

In this proof we were able to use $\Leftrightarrow$ all the way through, which is the shortest way. But often in proving two sets $A, B$ are equal it's necessary to show $A \subseteq B$ and $B \subseteq A$ separately, using one-way implications.