![$ E = \left[\begin{array}{ccccc}1&2&0&-1&0\\ 0&0&1&3&0\\ 0&0&0&0&1\end{array}\right]$](img45.gif) , as shown in
§3. A basis for the row space consists of the three nonzero rows
of
, as shown in
§3. A basis for the row space consists of the three nonzero rows
of
For Problem J-1:
In §2, row-reduce ![]() to get
to get
![$ E = \left[\begin{array}{ccccc}1&2&0&-1&0\\ 0&0&1&3&0\\ 0&0&0&0&1\end{array}\right]$](img45.gif) , as shown in
§3. A basis for the row space consists of the three nonzero rows
of
, as shown in
§3. A basis for the row space consists of the three nonzero rows
of ![]() .
.
In §5, make a matrix ![]() whose columns are the given vectors.
The linear relations between the columns are given by the null
space, so the possible coefficients
whose columns are the given vectors.
The linear relations between the columns are given by the null
space, so the possible coefficients
![]() are linear
combinations of the basis vectors from §3, namely
are linear
combinations of the basis vectors from §3, namely
![]() and
and
![]() (where they were columns, but here we can
write rows if we want to).
(where they were columns, but here we can
write rows if we want to).
In §7, based on the explanation we make ![]() with the given
vectors as columns and find a basis for the null space of
with the given
vectors as columns and find a basis for the null space of ![]() ,
which is the same as the matrix in §4 (called
,
which is the same as the matrix in §4 (called ![]() there, but
that's a different
there, but
that's a different ![]() from this problem). Then we transpose
back. The basis is the same as shown in §3, so our answer is
from this problem). Then we transpose
back. The basis is the same as shown in §3, so our answer is
![$ M = \left[\begin{array}{rrrrr}-2&1&0&0&0\\ 1&0&-3&1&0\end{array}\right]$](img51.gif) .
.
For Problem J-2:
For §8: Following the suggestion, let's put the two lists together as columns of a matrix. Then the problem is like §6, so one basis consists the first, third, and fifth of these vectors.
If you find the basis by instead making a matrix with these
five vectors as rows, when you row reduce you get the identity
matrix. This means that the rows generate all of
![]() ,
and the basis is the standard basis.
,
and the basis is the standard basis.
For §9: As mentioned, the idea is that when you throw two sets of equations together, the set of solutions in common is the intersection of their respective solution sets.
For the vectors
![]() , putting them as
the rows of a matrix and looking for a basis for the null space
we get a single basis vector. Any scaled version of it will do;
the simplest seems to be
, putting them as
the rows of a matrix and looking for a basis for the null space
we get a single basis vector. Any scaled version of it will do;
the simplest seems to be ![]() . We can check that this
vector is indeed in the null space.
. We can check that this
vector is indeed in the null space.
For the vectors
![]() , putting them as the rows
of a matrix we get a basis vector proportional to
, putting them as the rows
of a matrix we get a basis vector proportional to ![]() ,
so let's use that one. We take our two null-space bases
together as the rows of a matrix, whose null space should be the
intersection we desire. A basis for the null space is a single
vector proportional to
,
so let's use that one. We take our two null-space bases
together as the rows of a matrix, whose null space should be the
intersection we desire. A basis for the null space is a single
vector proportional to ![]() .
.
Although the problem doesn't ask us to, we could check that
our answer is in the span of both of the original spanning
sets. For ![]() we get
we get
![]() .
For
.
For ![]() ,
, ![]() is already one of the spanning
vectors in the second subspace.
is already one of the spanning
vectors in the second subspace.
For Problem J-3:
(a) For uniformity, let's write all vectors as column vectors
and then for a row vector write the transpose of a column vector.
Direction ``
![]() '': If
'': If
![]() then row
then row
![]() is the
is the ![]() -th entry of
-th entry of ![]() times the vector
times the vector ![]() .
Since all rows are proportional, the row space is spanned by
.
Since all rows are proportional, the row space is spanned by
![]() alone. Therefore the rank of
alone. Therefore the rank of ![]() is 1.
is 1.
Direction ``
![]() '':
Since
'':
Since ![]() is nonzero it has some row that is a nonzero row
vector; call it
is nonzero it has some row that is a nonzero row
vector; call it ![]() . Since
. Since ![]() is a nonzero vector in a
1-dimensional space (the row space), it spans the row space
and every vector in the space is a scalar times
is a nonzero vector in a
1-dimensional space (the row space), it spans the row space
and every vector in the space is a scalar times ![]() , in fact
a unique scalar since
, in fact
a unique scalar since ![]() is nonzero. Let
is nonzero. Let ![]() be
the scalar for row
be
the scalar for row ![]() and let
and let
![]() ,
where
,
where ![]() is the number of rows of
is the number of rows of ![]() . Then
. Then
![]() .
.
(b) The key observation is that elementary row operations preserve the property that the rows are arithmetic progressions. You can do this directly, but a nicer way is to point out that the differences of consecutive columns are all the same and that this is a linear relation between columns and so is preserved by row operations.
What matrices in row-reduced echelon form have the property that their
rows are in arithmetic progression? One possible row is
![]() .
Another is
.
Another is
![]() . Also possible is
. Also possible is
![]() . But that's
all, since all rows have 1 as their first nonzero entry, if any. So
the rank can't be more than 2.
. But that's
all, since all rows have 1 as their first nonzero entry, if any. So
the rank can't be more than 2.
For Problem J-4: (a) In this problem there are two numberings--the numbers used to name the fingers and the numbers of the terms in the sequence. The sequence repeats every 8, so we can work modulo 8. Since 8 divides 1,000,000 evenly, it's tempting to say the 0-th term is the same as the millionth, but since there was no 0-th term in this problem we look at the 8th term, which is finger number 2 (index finger).
(b) This problem really asks what number from 0 to 9 is congruent
to
![]() modulo 10. Working base 10, we simply
ignore all digits but the last.
modulo 10. Working base 10, we simply
ignore all digits but the last. ![]() ends in 9,
ends in 9, ![]() ends
the same as
ends
the same as ![]() , which is 1, and since
, which is 1, and since
![]() , the answer is 1.
, the answer is 1.
(c) See answers to (a) and (b).
For Problem J-5:
(a) We know
![]() , so
, so ![]() has the same number of elements
as
has the same number of elements
as ![]() , namely 4. In general, if
, namely 4. In general, if ![]() is the 2-element field
then
is the 2-element field
then ![]() will have
will have ![]() elements.
elements.
(b) For any field ![]() , if
, if ![]() are distinct 2-dimensional
subspaces of
are distinct 2-dimensional
subspaces of ![]() , then
, then
![]() is larger than
either, so must be the whole space, so is of dimension 3. Then
the equation
dim
is larger than
either, so must be the whole space, so is of dimension 3. Then
the equation
dim![]() dim
dim![]() dim
dim![]() dim
dim![]() becomes
becomes
![]() , so the
intersection must have dimension 1.
, so the
intersection must have dimension 1.
(c) If ![]() and
and ![]() are distinct 1-dimensional
subspaces, then their intersection is
are distinct 1-dimensional
subspaces, then their intersection is
![]() 0
0![]() , so the equation
dim
, so the equation
dim![]() dim
dim![]() dim
dim![]() dim
dim![]() shows that their sum has dimension 2.
Therefore
shows that their sum has dimension 2.
Therefore ![]() and
and ![]() are contained in just one
2-dimensional subspace.
are contained in just one
2-dimensional subspace.
(d) As suggested, let the 1-dimensional subspaces be the plants
and the 2-dimensional subspaces determine blocks (so the block
for ![]() of dimension 2 consists of the 1-dimensional subspaces
contained in
of dimension 2 consists of the 1-dimensional subspaces
contained in ![]() ). Then by (c), any two plants have exactly
one block in common, and by (b), any two blocks have exactly one
plant in common. This much would work over any field. For
GF(2), the solution to Problem G-4 shows precisely how to make
the actual design. For each block we get three plants in it,
since there are three 1-dimensional subspaces in each 2-dimensional
vector space over GF(2).
). Then by (c), any two plants have exactly
one block in common, and by (b), any two blocks have exactly one
plant in common. This much would work over any field. For
GF(2), the solution to Problem G-4 shows precisely how to make
the actual design. For each block we get three plants in it,
since there are three 1-dimensional subspaces in each 2-dimensional
vector space over GF(2).
For Problem J-6:
![]() for all
for all ![]() . For addition and multiplication we get
. For addition and multiplication we get
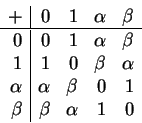 and
and
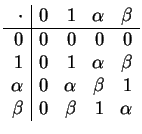
Therefore ![]() is closed under addition and multiplication.
It does turn out that multiplication is commutative, even though
for other
is closed under addition and multiplication.
It does turn out that multiplication is commutative, even though
for other
![]() matrices it might not be.
matrices it might not be.
(b) To see that ![]() is a field: Additively,
is a field: Additively, ![]() is a vector
subspace of the vector space of
is a vector
subspace of the vector space of
![]() matrices over GF(2),
so the laws involving addition, negation, and 0 hold. Multiplicatively,
the associative law is true for matrices in general,
matrices over GF(2),
so the laws involving addition, negation, and 0 hold. Multiplicatively,
the associative law is true for matrices in general, ![]() is
commutative as we saw, and the multiplication table shows that
each nonzero element of
is
commutative as we saw, and the multiplication table shows that
each nonzero element of ![]() has a multiplicative inverse. The
distributive law is true for matrices in general.
has a multiplicative inverse. The
distributive law is true for matrices in general.
(c) The characteristic is 2, since ![]() .
.
(d) Yes,
![]() has exactly the same operation
tables as
has exactly the same operation
tables as ![]() .
.
For Problem J-7:
In the addition table, consider the column for any element ![]() and rows for elements
and rows for elements ![]() and
and ![]() . If the
corresponding two entries in the column are the same, that
says
. If the
corresponding two entries in the column are the same, that
says
![]() . We are tempted to cancel
the
. We are tempted to cancel
the ![]() 's, and in fact that is ok since field have additive
inverses. Then
's, and in fact that is ok since field have additive
inverses. Then
![]() . This shows that two
different rows cannot have equal entries in a column.
Since the operation is commutative, each row also has distinct
entries. Thus the table is a Latin square.
. This shows that two
different rows cannot have equal entries in a column.
Since the operation is commutative, each row also has distinct
entries. Thus the table is a Latin square.
For the multiplication table, again we are asking whether
![]() . The
answer is yes, since in a field nonzero elements have
multiplicative inverses and so we can cancel the
. The
answer is yes, since in a field nonzero elements have
multiplicative inverses and so we can cancel the ![]() . Again
the operation is commutative so the rows also have distinct
entries. Thus the table is a Latin square.
. Again
the operation is commutative so the rows also have distinct
entries. Thus the table is a Latin square.
For Problem J-8:
(a) There are two things to show: That each table ![]() is a
Latin square and that any two tables are orthogonal.
is a
Latin square and that any two tables are orthogonal.
To see that each row of ![]() has distinct entries, look at
an arbitrary column
has distinct entries, look at
an arbitrary column ![]() and rows
and rows ![]() ,
, ![]() . Suppose
that
. Suppose
that
![]() . This says
. This says
![]() . Canceling the common
term we get
. Canceling the common
term we get
![]() , so there is no repeated
entry in the column.
, so there is no repeated
entry in the column.
We can't just say ``similarly,...'' for the rows, since the
definition of ![]() is not symmetrical for rows and columns!
So look at an arbitrary row
is not symmetrical for rows and columns!
So look at an arbitrary row ![]() and columns
and columns ![]() ,
, ![]() .
Suppose that
.
Suppose that
![]() . This says
. This says
![]() . Canceling
the common term we get
. Canceling
the common term we get
![]() . Since
. Since ![]() we can also cancel
we can also cancel ![]() and we get
and we get
![]() .
Therefore there is no repeated entry in the row. This finishes
the proof that
.
Therefore there is no repeated entry in the row. This finishes
the proof that ![]() is a Latin square, for any
is a Latin square, for any ![]() .
.
Now consider two squares ![]() and
and ![]() . Are they
orthogonal? This means that there are no two positions with the
same pair of entries. In other words, if
. Are they
orthogonal? This means that there are no two positions with the
same pair of entries. In other words, if
![]() , must
, must ![]() and
and ![]() ? Let's see: This says
? Let's see: This says
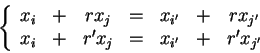
Putting everything on the left in each equation we get
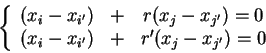
Subtracting and simplifying, we get
![]() .
Since
.
Since
![]() , we can cancel that factor and get
, we can cancel that factor and get
![]() ,
so
,
so
![]() . Then in the first equation of the
last pair we get
. Then in the first equation of the
last pair we get
![]() , so that
, so that
![]() , and we are done.
, and we are done.
(b) Using the order
GF![]() , the tables are
, the tables are
![$ \left[\begin{array}{cccc}0&1&\alpha&\beta\\ 1&0&\beta&\alpha\\ \alpha&\beta&0&1\\ \beta&\alpha&1&0\end{array}\right]$](img131.gif)
![$ \left[\begin{array}{cccc}0&\alpha&\beta&1\\ 1&\beta&\alpha&0\\ \alpha&0&1&\beta\\ \beta&1&0&\alpha\end{array}\right]$](img132.gif)
![$ \left[\begin{array}{cccc}0&\beta&1&\alpha\\ 1&\alpha&0&\beta\\ \alpha&1&\beta&0\\ \beta&0&\alpha&1\end{array}\right]$](img133.gif)
Using the equivalences suggested in the problem and superimposing the tables, we get the cards
| ASr | 2Ds | 3Cg | 4Hb |
| 2Hg | ACb | 4Dr | 3Ss |
| 3Db | 4Sg | AHs | 2Cr |
| 4Cs | 3Hr | 2Sb | ADg |
Here colors are lower case; S is spades and s is silver.