p. 5
Ex. 5. Comment: This describes addition and multiplication in
GF(2) =
![]() . Unary minus (negation) is
. Unary minus (negation) is ![]() . The
intended solution to the problem is to check each law. After
checking commutativity of addition and multiplication, you can
save some effort in checking associativity.
. The
intended solution to the problem is to check each law. After
checking commutativity of addition and multiplication, you can
save some effort in checking associativity.
Ex. 7: Suppose ![]() is a subfield of
is a subfield of
![]() . To be a field,
. To be a field,
![]() must contain 0 and 1 (the same 0 and 1 as in
must contain 0 and 1 (the same 0 and 1 as in
![]() , since
those are the only neutral elements for addition and multiplication).
Then
, since
those are the only neutral elements for addition and multiplication).
Then ![]() also contains
also contains
![]() and their negatives, so
and their negatives, so
![]() contains at least
contains at least
![]() . But to be a subfield
. But to be a subfield ![]() must
also contain the multiplicative inverse of each of its nonzero
elements, so
must
also contain the multiplicative inverse of each of its nonzero
elements, so ![]() contains
contains
![]() , etc.
Multiplying these in
, etc.
Multiplying these in ![]() by integers, we get all of
by integers, we get all of
![]() . In
other words,
. In
other words,
![]() .
.
Ex. 8: Let ![]() be any field of characteristic 0.
be any field of characteristic 0.
Informal version: In ![]() there is an element 1.
there is an element 1. ![]() is
like 2, so call it
is
like 2, so call it ![]() . Similarly, we can make
. Similarly, we can make
![]() ,
etc. Their negations are
,
etc. Their negations are ![]() , etc. If we fill out by
writing
, etc. If we fill out by
writing
![]() and
and
![]() , we have a copy of
of
, we have a copy of
of
![]() , sort of pseuo-integers. Their ratios make a copy of
, sort of pseuo-integers. Their ratios make a copy of
![]() .
.
There are a couple of issues here, though: First, where did we
use the fact that that characteristic is 0? The answer is that
to be sure about the copy of
![]() we need to know that the sums
of 1's and their negations are all distinct (i.e., different from
each other). For example, could
we need to know that the sums
of 1's and their negations are all distinct (i.e., different from
each other). For example, could
![]() ? Since
we can cancel additively in a field,
? Since
we can cancel additively in a field,
![]() would
imply
would
imply ![]() , which can't happen since the characteristic
is 0. In other words, by additive cancellation, if
, which can't happen since the characteristic
is 0. In other words, by additive cancellation, if
![]() ,
then
,
then
![]() , which for characteristic 0 implies
, which for characteristic 0 implies ![]() .
.
Another issue is whether the sums of 1's have operations like
those of integers. For example, do we have
![]() and
and
![]() ? Yes, the first left-hand side
is the sum of five 1's and
? Yes, the first left-hand side
is the sum of five 1's and
![]() , by the distributive law in
, by the distributive law in ![]() .
.
Since the problem is early in the book, most likely the authors
expected only an informal solution, but it's possible to be more
formal, as follows. A ``copy'' of
![]() means a subfield
isomorphic to
means a subfield
isomorphic to
![]() as a field, so we try to construct a one-to-one
function
as a field, so we try to construct a one-to-one
function
![]() , whose ``image'' will be a subfield of
, whose ``image'' will be a subfield of ![]() .
Let
.
Let
![]() . For an integer
. For an integer ![]() we define
we define
![]() .
(Here
.
(Here
![]() means
means ![]() , etc.)
As in the informal version we can check that
, etc.)
As in the informal version we can check that ![]() so far is
one-to-one and preserves addition and multiplication of integers.
so far is
one-to-one and preserves addition and multiplication of integers.
Now for any fraction
![]() with
with
![]() we
define
we
define
![]() to be
to be
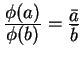 ,
meaning
,
meaning
![]() . But there is also an issue
here: Since different fractions can represent the same rational
number, e.g.,
. But there is also an issue
here: Since different fractions can represent the same rational
number, e.g.,
![]() , could we conceivably
get inconsistent values from our definition? Is
, could we conceivably
get inconsistent values from our definition? Is
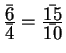 , necessarily? In other words, we
must check that if
, necessarily? In other words, we
must check that if
![]() then
then
![]() in
in ![]() . But it's OK:
. But it's OK:
![]() , as hoped. We say that ``
, as hoped. We say that ``![]() is well defined''.
is well defined''.
To finish the proof we need to check that ![]() preserves addition
and multiplication for rational numbers and is one-to-one. So far
we know this on
preserves addition
and multiplication for rational numbers and is one-to-one. So far
we know this on
![]() only. For
only. For
![]() we have
we have
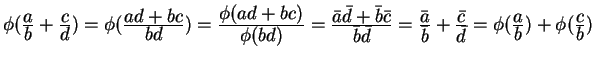 , which is the correct
result. Multiplication is checked similarly.
, which is the correct
result. Multiplication is checked similarly.
For being one-to-one, let's see if
![]() implies
implies
![]() :
:
![]() says
says
![]() , so
, so
![]() , or
, or
![]() . Since
we know
. Since
we know ![]() is one-to-one for integers,
is one-to-one for integers, ![]() , so
, so
![]() as hoped.
as hoped.
p. 33
Ex. 1 (outline). The various properties come from similar properties
of ![]() (which you can quote) and from the fact that operations in
(which you can quote) and from the fact that operations in
![]() are defined coordinatewise.
are defined coordinatewise.
Ex. 5. ![]() is not commutative or associative. We do have
is not commutative or associative. We do have
![]() 0
0![]() , though, and for each
, though, and for each ![]() ,
,
![]() 0,
so
0,
so ![]() is its own additive inverse. Also,
is its own additive inverse. Also,
![]() rather than
rather than ![]() , so (4a) fails. But (4b), (4c), (4d) hold, since
in each case both sides have the same number of minuses when
rewritten using ordinary multiplication by scalars.
, so (4a) fails. But (4b), (4c), (4d) hold, since
in each case both sides have the same number of minuses when
rewritten using ordinary multiplication by scalars.
p. 39
Ex. 1. Just (b) is a subspace. (a) is not closed under multiplication by negative scalars; (c) is not closed under addition nor under multiplication by scalars; (d) is not closed under addition; (e) is not closed under multiplication by scalars, since irrational scalars don't work.
Ex. 2. (b), (d), and (e) are subspaces. This may seem surprising,
but they work because operations on functions are defined pointwise.
Saying ![]() , for example, is somewhat like saying
, for example, is somewhat like saying ![]() for
for
![]() .
.
For (e), we need to quote the theorems that the sum of two continuous functions is continuous and that a continuous function times a constant is continuous.
(a) is not a subspace because the constant function 1 is in the set but twice it (the constant function 2) is not. (c) is not a subspace because the 0 function (constant 0) is not in it.
Ex. 3. Method #1: Outline: Write the first vector as a linear combination of the others with unknown coefficients, make linear equations, and solve.
Method #2: Make the vectors the columns of a matrix ![]() ,
with the ``target'' vector as the last column, and row reduce to a
matrix
,
with the ``target'' vector as the last column, and row reduce to a
matrix ![]() in row-reduced echelon form. Since the linear
relations between the columns don't change, you can check in
in row-reduced echelon form. Since the linear
relations between the columns don't change, you can check in
![]() to see whether the last column is in the span of the
preceding ones (and if so, with what coefficients), and the same
will hold for columns of
to see whether the last column is in the span of the
preceding ones (and if so, with what coefficients), and the same
will hold for columns of ![]() . Notice, though, that
. Notice, though, that ![]() and
and
![]() are exactly the same as what you get in Method #1.
are exactly the same as what you get in Method #1.
Ex. 4. This is asking for a basis of the solution space of the homogeneous equations, which is the same thing as a basis of the null space of the matrix of coefficients. Row reduce, etc.
Ex. 5. Just (c) is a subspace. The set of matrices in (c) contains
the zero matrix and is closed under multiplication by scalars. It is
also closed under addition, since if ![]() are in the set,
we have
are in the set,
we have
![]() .
.
Notice that matrix multiplication is used in defining the subspace but is not used for operations on the vector space of matrices involved.
For (a), the zero matrix is not in the set. For (b), the sum of
two noninvertible matrices could be invertible, e.g,
![$ \left[\begin{array}{rr}1&0\ 0&0\end{array}\right]
+ \left[\begin{array}{rr}0&0\ 0&1\end{array}\right] = \left[\begin{array}{rr}1&0\ 0&1\end{array}\right]$](img63.gif) . (Here it's important that
. (Here it's important that
![]() .) For (d), the set is not closed under multiplication by 2.
.) For (d), the set is not closed under multiplication by 2.
p. 48
Ex. 1. If ![]() and
and ![]() are linearly dependent, there is a
nontrivial linear relation
are linearly dependent, there is a
nontrivial linear relation
![]() 0. Nontrivial means
that
0. Nontrivial means
that ![]() or
or ![]() or both. If
or both. If ![]() we can
solve to get
we can
solve to get
![]() , so that
, so that ![]() is a scalar
multiple of
is a scalar
multiple of ![]() . If
. If ![]() , a similar proof applies the
other way around.
, a similar proof applies the
other way around.
Ex. 2. Method: Make a matrix with these as either the rows or the columns and row reduce. If you get the identity matrix, so the rank is 4, then they are linearly independent; otherwise not.
Ex. 3. Method #1: Make a matrix with the four vectors as rows and row-reduce. The nonzero rows of the row-reduced echelon form are a basis for the row space.
Method #2: Make a matrix with the four vectors as columns and row-reduce. See which columns are pivot columns. The same-numbered columns of the original matrix are a basis for the column space.
Ex. 4. If you were asked only to show that the vectors form a basis, you could do this like Ex. 2 above. Since you are asked also to express the standard basis vectors relative to this basis, you might as well do that first and then you will have shown that these vectors form a basis.
Naive method: Try
![]() , which results in three equations in the three
unknowns, which you can solve by row reduction. Then do the
same for
, which results in three equations in the three
unknowns, which you can solve by row reduction. Then do the
same for ![]() and
and ![]() , each time getting new values for
the coefficients.
, each time getting new values for
the coefficients.
Organized method: Make a matrix with these three vectors as the
first three columns and
![]() as the last three columns,
so the matrix looks like
as the last three columns,
so the matrix looks like ![]() . Row reduce. You should
get a matrix that looks like
. Row reduce. You should
get a matrix that looks like ![]() . Since linear relations
between columns are preserved, looking at each column of the
. Since linear relations
between columns are preserved, looking at each column of the ![]() part as a linear combination of the first three columns tells you
how to represent each of
part as a linear combination of the first three columns tells you
how to represent each of
![]() as a linear combination
of columns of
as a linear combination
of columns of ![]() . (Note. Actually
. (Note. Actually
![]() in this
situation.)
in this
situation.)
Ex. 5. Take three vectors in a plane, such as ![]() ,
,
![]() ,
, ![]() .
.
Ex. 6. Thinking of the
![]() matrices as
matrices as
![$ \left[\begin{array}{rr}r&s\ t&u\end{array}\right]$](img83.gif) ,
,
![]() can be described by
can be described by ![]() and
and ![]() can be
described by
can be
described by ![]() .
.
(a) Both of these equations are preserved
under addition of matrices and multiplying matrices by scalars.
Also both contain the zero matrix. So
![]() are
subspaces of
are
subspaces of ![]() .
.
(b) Intuitively, each of ![]() and
and ![]() involves
choosing three parameters freely, so their dimensions ought to be 3.
More officially, a basis for
involves
choosing three parameters freely, so their dimensions ought to be 3.
More officially, a basis for ![]() consists of the matrices
you get by choosing one parameter to be 1 and the others 0:
consists of the matrices
you get by choosing one parameter to be 1 and the others 0:
![$ \left[\begin{array}{rr}1&-1\ 0&0\end{array}\right]$](img90.gif) ,
,
![$ \left[\begin{array}{rr}0&0\ 1&0\end{array}\right]$](img91.gif) , and
, and
![$ \left[\begin{array}{rr}0&0\ 0&1\end{array}\right]$](img92.gif) .
Similarly, a basis for
.
Similarly, a basis for ![]() consists of
consists of
![$ \left[\begin{array}{rr}1&0\ -1&0\end{array}\right]$](img93.gif) ,
,
![$ \left[\begin{array}{rr}0&1\ 0&0\end{array}\right]$](img94.gif) , and
, and
![$ \left[\begin{array}{rr}0&0\ 0&1\end{array}\right]$](img92.gif) .
.
Since each of
![]() consists of linear combinations of
the respective basis matrices,
consists of linear combinations of
the respective basis matrices,
![]() consists of
linear combinations of all six, or really five since one is repeated.
But the five are dependent--obviously, since we are in the space
consists of
linear combinations of all six, or really five since one is repeated.
But the five are dependent--obviously, since we are in the space ![]() of dimension 4. One way to determine the actual dimension is to use an
isomorphism of
of dimension 4. One way to determine the actual dimension is to use an
isomorphism of ![]() with
with
![]() , let's say
, let's say
![$ (r,s,t,u) \mapsto
\left[\begin{array}{rr}r&s\ t&u\end{array}\right]$](img97.gif) . We are then asking about five 4-tuples. Make
a matrix with the five as its rows or columns, row-reduce, and see what
the rank is. You should get 4. Another way is that since
. We are then asking about five 4-tuples. Make
a matrix with the five as its rows or columns, row-reduce, and see what
the rank is. You should get 4. Another way is that since ![]() has dimension 3 in a space
has dimension 3 in a space ![]() of dimension 4, if you just notice that
the first basis vector of
of dimension 4, if you just notice that
the first basis vector of ![]() is not in
is not in ![]() , their
sum must be larger than
, their
sum must be larger than ![]() , so all of
, so all of ![]() .
.
For
![]() , go back to the equations in
, go back to the equations in ![]() .
We have
.
We have
![]() , which
, which ![]() varies freely, so the general
form of a matrix in this subspace is
varies freely, so the general
form of a matrix in this subspace is
![$ \left[\begin{array}{rr}r&-r\ -r&u\end{array}\right]$](img102.gif) . A
basis is
. A
basis is
![$ \left[\begin{array}{rr}1&-1\ -1&0\end{array}\right]$](img103.gif) and
and
![$ \left[\begin{array}{rr}0&0\ 0&1\end{array}\right]$](img92.gif) , so the
space has dimension 2.
, so the
space has dimension 2.
Another way would be to use the equation
dim![]() dim
dim![]() and
solve
and
solve
![]() , getting
, getting ![]() .
.
Ex. 9. See the solution of D-1 below. With the isomorphism method
you get vectors ![]() ,
, ![]() ,
, ![]() in
in
![]() .
Put them as the rows of a matrix and row reduce; you get the identity
matrix, so the rank is 3 and the original rows were linearly independent.
.
Put them as the rows of a matrix and row reduce; you get the identity
matrix, so the rank is 3 and the original rows were linearly independent.
Ex. 12. A basis consists of the ![]() matrices each with one entry
of 1 and the rest 0's. One way to see this is that if you use
an isomorphism with
matrices each with one entry
of 1 and the rest 0's. One way to see this is that if you use
an isomorphism with
![]() , these matrices correspond
to the standard basis.
, these matrices correspond
to the standard basis.
For Problem B-1:
All are like
![]() . For example, (g) says
. For example, (g) says ![]() is a
necessary condition for
is a
necessary condition for ![]() . This means that if
. This means that if ![]() is true,
then
is true,
then ![]() , being necessary for
, being necessary for ![]() , also has to be true.
So
, also has to be true.
So
![]() .
.
For Problem B-2: Each of (1), (4), (5) implies the others (and itself, for that matter). Each of (2), (3) implies the other (and itself). Each of (1), (4), (5) implies each of (2), (3).
For Problem B-3:
Neither of (2), (3) implies any of (1), (4), (5); a counterexample in
each case is ![]() .
.