2. The solution space to a set of homogeneous linear equations

Problem. Find a basis for the solution space of

$$\begin{array}{rrrrrrrrrrrrr} x &+& 2y &+& z &+& 2s &+& 3t &=... ...t &=& 0\\ x &+& 2y &+& 3z &+& 8s &+& 8t &=& 0\\ \end{array}$$

Solution. Don't bother to augment $M$ with a constant column, since it would be all 0's and would stay that way during row reduction. Just row-reduce $M$ itself, getting

$E = \left[\begin{array}{ccccc}1&2&0&-1&0\\ 0&0&1&3&0\\ 0&0&0&0&1\end{array}\right]$.

The non-pivot variables are $y$ and $s$. The general solution is

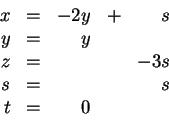$$\begin{array}{rrrrr} x &=& -2y &+& s \\ y &=& y \\ z &=& & & -3 s \\ s &=& & & s \\ t &=& 0\\ \end{array}$$, or equivalently, $\left[\begin{array}{r}x\\ y\\ z\\ s\\ t\end{array}\right] = y \left[\begin... ...rray}\right] + s \left[\begin{array}{r}1\\ 0\\ -3\\ 1\\ 0\end{array}\right]$.
The basis, then, consists of these two column vectors.