Oscillator labs

As usual, Netscape may work better than Internet Explorer for these.

A (single) harmonic oscillator means motion obeying

$$a(t) = -k x(t),$$

where $k$ is a positive constant. In other words, acceleration is proportional to position, but negatively, so that the moving point is always being pushed back towards the origin. Since acceleration is the second derivative of position, the DE says

$$x'' = -k x.$$

The general solution is

$$x(t) = c _ 1 \cos(\sqrt k \; t) + c _ 2 \sin(\sqrt k \; t),$$

so the motion is periodic. The period $T$ is the length of time for $\sqrt k \; t$ to go from 0 to $2 \pi$, so

$$T = \frac {2 \pi} {\sqrt k}.$$

The motion is called ``harmonic'' because if this vibration is used for sound, you get a pure pitch, sounding like blowing across a bottle or whistling a steady tone.

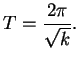
If we consider ``linked'' harmonic oscillators, where there are two or more oscillators and the acceleration of each depends on the position of all of them, the motion gets much more complicated--and yet it is easily understood using eigenvalues.

Problem FF-1. Try the ``double oscillator demo'' on the course home page.

The double oscillator represents two linked harmonic oscillators:

$$\left \{ \begin{array}{ccc} x'' &=& p x + q y \\ y'' &=& r x + s y \end{array} \right .$$

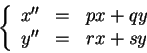
or for short, x$'' = M$   x. This motion can be nonperiodic and seemingly crazy, but there is an underlying regularity exposed by the eigenvectors.

View 1: You see just the oscillators, going crazy, never repeating.

View 2: Oscillators and acceleration vectors. Still crazy.

View 3: Positions shown on perpendicular axes, so that the coordinates of one moving dot can represent positions of both oscillators at once.

View 4: Shows track of the dot. Let it go for a while. Now it becomes clearer that there is some regularity.

View 5: Shows position and acceleration vectors. Not so clear again.

View 6: Shows position and acceleration vectors and their components on eigenspaces. Notice that the components are periodic, but of different periods. In other words, the crazy motion is really the vector sum of two periodic motions of incompatible periods.

In this view, you can click on ``Set'', drag the red dot to any position you wish, and click on ``Go'' to resume. Remember, doing this is equivalent to starting eachof the original two oscillators in position.

Write down what happens when you put the red dot on an eigenspace and then resume. Try both eigenspaces. Are the periods the same? If you back up to the initial view, you should see the same periodic motion.

Note. This demo is purely visual. However, these DE's can be diagonalized just like a first-order system. The eigenvalues are negative and play the role of $k$ in the single oscillator solution. Thus the eigenvalues determine the periods of the two underlying periodic oscillations. Specifically, each eigenvalue $\lambda < 0$ is like $-k$, so

$$T = \frac {2 \pi}{\sqrt{- \lambda}}.$$

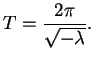
Problem FF-2. Try the ``multiple oscillator demo'' on the course home page. Having selected it, click on the bar to start it. You should see four linked oscillators, obeying $x'' = Ax$ for a random symmetric matrix $A$ with negative eigenvalues. The motion will be non-periodic. The purpose of this demo is to see that you get periodic motion when the initial conditions correspond to an eigenvector.

(a) Try stopping the motion with ``Set'', dragging one or more of the dots to a new position, and restarting with ``Go''. Does that have much effect on the kind of motion, e.g., faster or slower?

(b) Go ``Forward'' to see the matrix. Diagonalize the matrix and select a column of $P$ (an eigenvector). Then go back. You will see the same motion but with arrows representing the four coordinates of the eigenvector.

Stop the motion, drag the dots to the arrows, and restart. You should see periodic motion.

(c) Repeat (b) for a different column (eigenvector). Does that affect the period? It should, since the eigenvalue for that eigenvector determines the period, as described above.