Assignment #2

Office hours: These will now be Monday 1:30-2:30, Tuesday 1:30-2:30, and Thursday 2:30-3:30.

Quiz 2 in discussion section, Tuesday, October 9: You will be asked to do some proof from p. 31.

Assignment due in lecture Wednesday, October 10:

where	Do but don't hand in	Hand in
p. 5		8
p. 48	1, 2, 5, 12	3, 4, 7, 9
E	E-3, E-5, E-6	E-1, E-2, E-4, E-7, E-8

Problem E-1. Show that if $u, v, w \in V$ are linearly independent, so are $u, u+v, u+v+w$.

Problem E-2. Over GF(2) (in other words, over $\mathbb{Z}_2$), solve these simultaneous equations, if that's possible, and check your answer:

$$\begin{array}{rrrrrrrrr} x &+& & & z &+& &=& 0 \\ & & & &... ...y & & &+& w &=& 0 \\ & & y &+& z & & &=& 1 \\ \end{array}$$

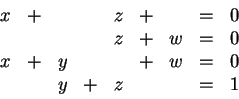
Problem E-3. Over $\mathbb{R}$, for the matrix

$$M = \left(\begin{array}{rrrrr} 1& 2& 1& 3& -2\\ 1& 2& 2& 3& 0\\ 1& 2& 3& 3& 2 \end{array}\right),$$

find a basis for (a) the row space, (b) the column space, and (c) the null space.

(Method: Row reduction doesn't change the row space or the null space, and it doesn't change the linear relations between columns. Careful, though: It does change the column space.)

Problem E-4. A function $f:S\rightarrow T$ (where $S$ and $T$ are any sets) is said to be ``one-to-one'' if distinct $s_1, s_2 \in S$ go to distinct values $f(s_1), f(s_2) \in T$; in other words, $f(s_1) = f(s_2) \Rightarrow s_1 = s_2$.

The function $f$ is said to take $S$ ``onto'' $T$ (``$f$ is onto'') if every element of $T$ is the image of some element of $S$; in other words, for each $t \in T$ there is at least one $s \in S$ with $f(s) = t$.

If $f$ is both one-to-one and onto, then $f$ is said to be a ``one-to-one correspondence'' between $S$ and $T$. In other words, each element of $S$ corresponds to exactly one element of $T$ and vice versa. In this case, there is an ``inverse function'' $f ^ {-1}:T\rightarrow S$ that undoes $f$ and is also a one-to-one correspondence.

In the following examples, say whether $f$ is one-to-one, onto, or both.

(a) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = x^3$.

(b) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = x^2$.

(c) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = x^3 - x$.

(d) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = \sin x$.

(e) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = e^x$.

(It may be helpful to think of the graphs of these functions.)

Problem E-5. Prove that if $f:S\rightarrow T$ is a one-to-one correspondence, so is the function $g:T\rightarrow S$ defined by saying $g(t)$ is the unique $s \in S$ for which $f(s) = t$. (Therefore we can define $f ^ {-1}$ to be this $g$.)

Problem E-6. A function between vector spaces is usually called a ``transformation''. A transformation $T:V\rightarrow W$ between vector spaces is said to be a linear transformation if it is compatible with the vector space operations, in the sense that

$T(v_1 + v_2) = T(v_1) + T(v_2)$ for every $v_1, v_2 \in V$, and

$T(rv) = rT(v)$ for every $r \in F$ and $v \in V$.

An $isomorphism$ of vector spaces $V$ and $W$ is a linear transformation $T:V\rightarrow W$ that is also a one-to-one correspondence. In that case, we say that $V$ and $W$ are isomorphic and we write $V \cong W$.

Examples:

• $\mathbb{R}^4 \cong$   Mats$(2,2)$.

• Since polynomials of degree at most 2 have the form $a+bx + cx^2$, $\mathbb{R}^3 \cong$   Pols$(\mathbb{R},2)$, using $T:\mathbb{R}^3 \rightarrow$   Pols$(\mathbb{R},2)$ defined by $T(a,b,c) = a + bx + cx^2$.

• Or, we could use a different isomorphism: $U:\mathbb{R}^3 \rightarrow$   Pols$(\mathbb{R},2)$ defined by $U(a,b,c) = ax^2 + bx + c$.

If two vector spaces are isomorphic, then anything we can say about vectors in one can be transferred over to vectors in the other.

The problem: Prove that if $T:V\rightarrow W$ is an isomorphism, then so is $T^{-1}$.

Problem E-7. Re-do Problem C-5, parts (b) and (c), using the idea of isomorphism. The shorter your answers, the better!

Problem E-8. (a) Find the mystery $3 \times 6$ matrix $A$ with entries in $\mathbb{R}$ if

(i) $A$ is in row-reduced echelon form;

(ii) each of columns 1, 3, 5 of $A$ is not in the span of the preceding columns;

(iii) column 2 of $A$ is 3 times column 1; column 4 is 2 times column 1 plus 5 times column 3; and column 6 is minus column 1 plus 7 times column 3 minus 4 times column 5.

(b) Explain: A matrix in row-reduced echelon form is uniquely determined by knowing what linear relations hold between its columns. (You can give an informal explanation, rather than trying to give careful descriptions of matrices in row-reduced echelon form, but do mention all important issues.)

(c) It is a fact that row reduction of a matrix does not affect linear relations between columns. Using this fact and (b), prove that the row-reduced echelong form of a matrix is unique. In other words, if two people independently row-reduce a matrix to row-reduced echelon form, they must get the same answer!