3. An application

A quadratic expression such as $6 x ^ 2 + 4 x y + 9y ^2$ is said to be a ``quadratic form''.

A quadratic form can be rewritten as x$^ t A$   x, where $A$ is symmetric and x$= \left[\begin{array}{c}x\\ y\end{array}\right]$ (a column vector) so x$^ t$ is a row vector. For example, $6x ^ 2 + 4 xy + 9y ^ 2 = \left[\begin{array}{cc}x&y\end{array}\right] \left[\b... ...{rr}6&2\\ 2&9\end{array}\right] \left[\begin{array}{c}x\\ y\end{array}\right]$. (Try multiplying out to check.) The coefficient of $xy$ is split in half and each half becomes an off-diagonal entry.

To analyze the graph of an equation such as $6x ^ 2 + 4xy + 9y ^ 2 = 1$, write it in matrix form, diagonalize the matrix, and make the substitution x$= R$r, where $R$ is a rotation matrix.

Example: Describe the graph of $3 x ^ 2 + 2 x y + 3 y ^ 2 = 1$.

Solution: Rewrite as x$^ t A$   x$= 1$ for $A = \left[\begin{array}{cc}3&1\\ 1&3\end{array}\right]$. We saw that $R ^ {-1} A R = D$ for $R = R _ {45 ^ \circ}$ and $D = \left[\begin{array}{rr}4&0\\ 0&2\end{array}\right]$. Substitute in x$= R$   r. We get $(R$r$) ^ t A (R$r$) = 1$, or r$^ t (R ^ t A R)$   r$= 1$. Since $R ^ t = R ^ {-1}$, we get r$^ t D$   r$= 1$, or $4 r ^ 2 + 2 s ^ 2 = 1$. This can be rewritten as

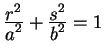${\frac{\displaystyle r ^ 2}{\displaystyle a ^ 2}} + {\frac{\displaystyle s ^ 2}{\displaystyle b ^ 2}} = 1$ for $a = {\frac 1 2}$, $b = {\frac 1 2}\sqrt 2$,

so the shape is an ellipse with semimajor axis ${\frac 1 2}\sqrt 2$ and semiminor axis ${\frac 1 2}$. But the ellipse is slanted. How? Since $a < b$, the end of the semimajor axis is where $r = 0$, $s = b = {\frac 1 2}\sqrt 2$; here x$= R \left[\begin{array}{c}0\\ {\frac 1 2}\sqrt 2\end{array}\right] = [$v$_ 1 \vert$   v$_ 2] \left[\begin{array}{c}0\\ {\frac 1 2}\sqrt 2\end{array}\right] = {\frac 1 2}\sqrt 2$   v$_ 2$, where v$_ 2$ is the second eigenvector, which is the same as the second column of $R$. Therefore the end of the semimajor axis of $R$ is at ${\frac 1 2}\sqrt 2 \left[\begin{array}{c}-{\frac 1 2}\sqrt 2\\ {\frac 1 2}\sq... ...y}\right] = \left[\begin{array}{c}-{\frac 1 2}\\ {\frac 1 2}\end{array}\right]$. You can check that this point is on the graph.

Problem DD-7. In this example, find the end of the semiminor axis.

Problem DD-8. (a) In general, the transformed equation is $\lambda _ 1 r ^ 2 + \lambda _ 2 s ^ 2 = 1$. Explain why, by discussing the substitution.

(b) How can you tell from the eigenvalues whether the equation is going to be an ellipse or a hyperbola or maybe some degenerate case? (In fact, what kinds of graphs can arise from (a)?)

Problem DD-9. (a) Describe the shape of the graph of $6x ^ 2 + 4xy + 9y ^ 2 = 1$. If it is an ellipse, give semimajor and semiminor axis lengths. (For this you can use eigenvalues alone.)

(b) How is this graph slanted? (You'll need the eigenvectors.)