0. Rotations

Definition. A list of vectors in R$^ n$ is orthonormal if the vectors are mutually perpendicular and all of length 1.

It can be shown that orthonormal vectors are linearly independent.

Recall that you can test perpendicularity (orthogonality) of two vectors by checking that their dot product is 0; also, the dot product of a vector with itself is its length squared. Therefore:

Vectors v$_ 1,\dots,$   v$_ n$ are orthonormal $\Leftrightarrow$ $\langle$   v$_ i,$   v$$_ j \rangle = \left \{ \begin{array}{lll} 1 & \mbox{if} & i=j\\ 0 & \mbox{if} & i \neq j \end{array}\right .$$

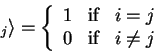
Definition. An $n \times n$ matrix $R$ is a rotation matrix if

(i) the columns of $R$ are orthonormal, and

(ii) $\det R = 1$.

For $2 \times 2$ matrices, rotations are just what you are used to, $R _ \theta$. However, using (i) and (ii) you can tell if a matrix is a rotation matrix without knowing the angle. For example, $R = \left[\begin{array}{rr}\frac 35&-\frac 45\\ \frac 45& \frac 35\end{array}\right]$ is a rotation, as you can check.