


Next: d_vsp
Up: d_vsp
Previous: d_vsp
3. Notes
- In the laws, we really mean that the equations are true
for all values of
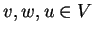 and all
and all
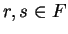 .
.
- Notice that (a)-(d) are about addition only (an ``additive
group''), while (e)-(h) involve multiplication by scalars.
- The text's definition of a vector space mentions
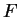 as if it is part of the vector space: ``A vector space
consists of a field
as if it is part of the vector space: ``A vector space
consists of a field 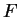 and a set
and a set 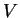 such that ...''. That's a
little old-fashioned. The difference is only technical.
such that ...''. That's a
little old-fashioned. The difference is only technical.
- Don't get confused between the zero scalar and the zero vector.
I'll usually write the 0 vector as
0 or
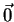 . In
. In
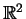 , for example, these are 0 and
0
, for example, these are 0 and
0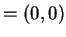 .
.
- The operation minus as mentioned above is ``unary'':
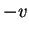 .
However, it is easy to define binary minus by saying
.
However, it is easy to define binary minus by saying  is
is
 .
.
- A binary operation is really a function on pairs. Addition
is a function
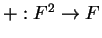 , while multiplication by scalars is
a function
, while multiplication by scalars is
a function
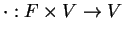 .
.
- In the course it will eventually become clear why all the
laws of
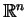 follow from the basic laws listed.
follow from the basic laws listed.
- These various laws together really say that for algebra
with scalars and vectors you can ``do what comes naturally''.
In this course you are free to do algebra on scalars and vectors
without explanation--except when we're talking about proving
some laws from others!



Next: d_vsp
Up: d_vsp
Previous: d_vsp
Kirby A. Baker
2001-10-09