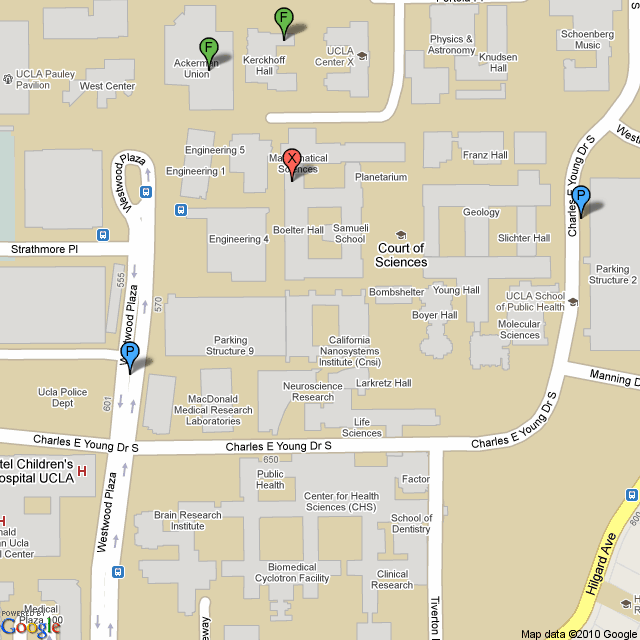
Location: Mathematical Sciences building, MS 6627
Schedule:
Saturday, Mar 9
8:00-9:00 Breakfast
9:00-10:00 Young-Heon Kim, University of British Columbia: On a multi-marginal optimal transport problem
I will discuss an optimal transport problem arising when there are many mass distributions to match together in a cost efficient way, explaining a work in progress with Brendan Pass. This talk will be introductory.
10:30-11:30 Oana Pocovnicu, Princeton: Scattering for a cubic-quintic nonlinear Schrodinger equation on R^3
In this talk, we consider the cubic-quintic nonlinear Schrodinger equation (NLS) on R^3 whose nonlinearity is given by the sum of a defocusing quintic power and a focusing cubic power. Notice that the quintic nonlinearity is energy-critical on R^3, while the cubic one is energy-subcritical. We consider the issue of scattering for the cubic-quintic NLS.
Previously, Tao, Visan, and Zhang proved global well-posedness in H^1 and scattering for solutions with small mass. The main result in this talk is scattering for solutions that are situated below a branch of (rescaled) solitons in the mass-energy plane. Moreover, we show that this region is a
maximal connected region near the origin where the virial is positive. Our result shows that while all solutions exist globally in time, the region of scattering is bounded by (rescaled) solitons, namely the situation is very different from the energy-critical defocusing/focusing quintic NLS. Our proof combines variational arguments and concentration-compactness and rigidity arguments. This is joint work with Rowan Killip (UCLA), Tadahiro Oh (Princeton University), and Monica Visan (UCLA).
11:30-1:00 Lunch
1:00-2:00 Zaher Hani, Courant: A continuum large-box limit for periodic NLS
Inspired by the general paradigm of weak turbulence theory, we consider the 2D cubic nonlinear Schrodinger equation on a box of size L with periodic boundary conditions. In an appropriate "large box regime" (L very large), we derive a continuum equation on $\R^2$ that governs the dynamics of the discrete frequency modes over certain nonlinear time scales. This equation turns out to satisfy some surprising symmetries and conservation laws, as well as several families of explicit solutions. (This is joint work with Erwan Faou (INRIA, France) and Pierre Germain (Courant Institute, NYU)).
2:30-3:30 Ioan Bejenaru, UCSD: Global solutions for equivariant Schroedinger Maps
I will discuss the problem of global well-posedness for equivariant Scroedinger Maps with energy below the natural threshold both in the focusing (maps to S^2) and defocusing case (maps to H^2).
3:30-4:00 Tea
4:00-5:00 Nets Katz, Caltech: On the slightly supercritical Navier Stokes equation
in the plane
We prove global solvability for the slightly supercritical Navier Stokes equation in the plane
generalizing a result of Tao from higher dimensions. We do this by replacing the equation with a system of differential inequalities for the amount of energy in various scales. We discuss why more
optimistic heuristics seem not to work and we discuss the significance of and open problems about the Besov norm with which we work.
There will be informal groups going out to dinner on Saturday evening (see below).
Sunday, Mar 10
8:00-8:30 Breakfast
8:30-9:30 Daniel Tataru, UC Berkeley, The energy critical Maxwell-Klein-Gordon equation
We consider the small data Maxwell-Klein-Gordon equation in 4+1 space dimensions. This is an energy critical problem, for which we can prove a global well-posedness result. This is joint work with Joachim Krieger and Jacob Sterbenz.
9:45-10:45 Stephen Gustafson, UBC, Global solutions for equivariant heat flow
I will present a global regularity result for the equivariant, higher-degree, above-threshold harmonic map heat-flow, which extends to higher energies earlier work with Nakanishi and Tsai on the heat and Schroedinger flows. This is work in progress with Dimitris Roxanas.
11:15-12:15 Rupert Frank (Caltech): Simplicity of eigenvalues of fractional Schroedinger operators
We prove that eigenvalues of fractional Schroedinger operators with radially increasing potentials are simple in each sector of angular momentum. The second eigenfunction in each sector has exactly one node. We also explain how this result implies the uniqueness (up to translations) of ground states of the non-local, non-linear equation (-\Delta)^s Q - Q^{\alpha+1}= - Q.
The talk is based on joint work with E. Lenzmann and L. Silvestre.
There will be an informal (free) registration during the conference.
A list of hotels near UCLA can be found here. A campus map can be found here.
Thanks to NSF grant DMS-0649473, we now have some funds to support graduate student and postdoctoral travel to attend this conference. Please contact tao@math.ucla.edu for details on this (or for any other inquiries). Reimbursement forms will be provided at the conference.
To get to campus, consult this Google map, centered on the Westwood Blvd parking booth.
Here is a map to help with on-campus navigation:

Key:
X = Location of lectures: Math Sciences building, room 6627.
P = Parking: (1) Parking booth on Westwood Plaza (=Blvd). (2) Self-service parking entrance to structure #2.
F = On-campus food: Kerckhoff coffee house (salads/sandwiches) and Ackerman Union (Sbarro/Panda Express/Carls Jr./Rubio's)
There are numerous eateries in Westwood village and further down Westwood Blvd. Here is a selection:
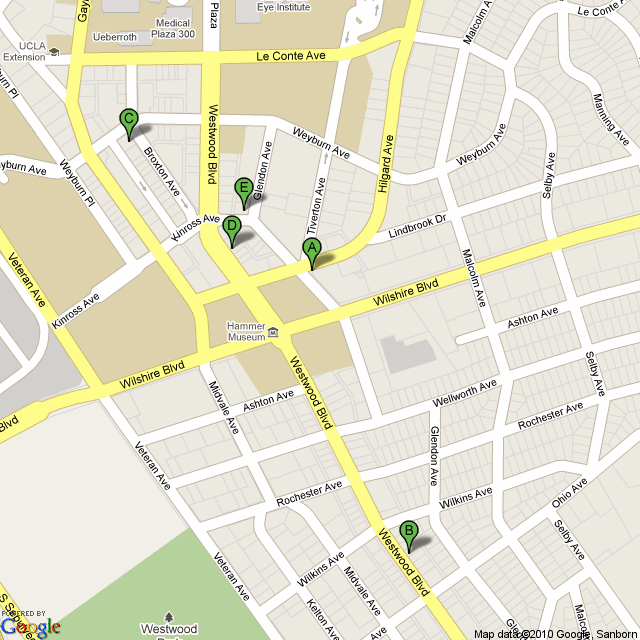
A = Palomino Very nice, but a little pricey.
B = Flame Persian Cuisine One of several Persian restaurants; this neighbourhood is known as "Little Persia".
C = California Pizza Kitchen Pizza.
D = Noodle Planet Very economical.
E = Westwood Brewing Co It's a bar.
Local organisers: Mario Bonk, John Garnett, Rowan Killip, Inwon Kim, Terence Tao, Monica Visan
Global organiser: Jacob Sterbenz
Previous SCAPDE meetings: