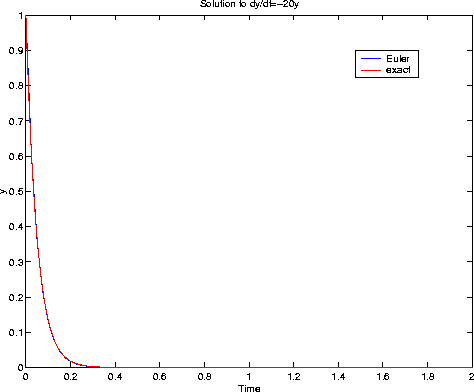
h=0.025
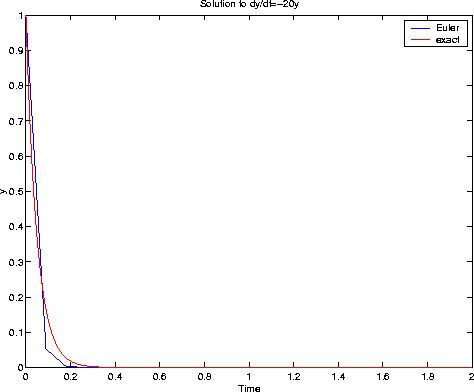
h=0.09
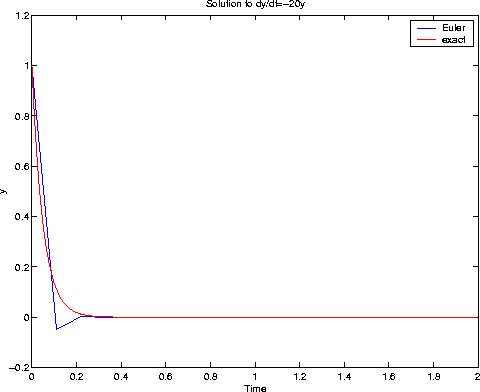
h=0.11
Let's compare the solutions obtained with the Trapezoidal Method, and with a simple
explicit method (in this case: Euler's Method). We will do this for different timesteps.
A simple script that
can be downloaded here .
Again, it uses the functions
deriv.m and
exact.m .
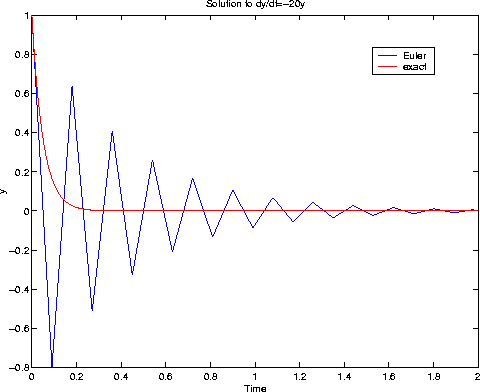
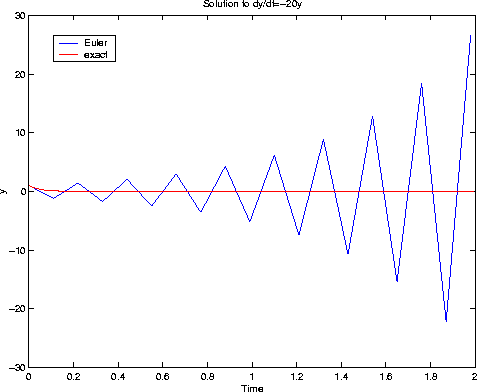
Clearly, the solution is unstable in the last case; in particular, it diverges. In the second case (h=0.09) the solution still oscillates (not very good !!), but at least the asymptotic behaviour (decay) is correct. We get a "pretty good" result for h=0.025.
h=0.025

h=0.09

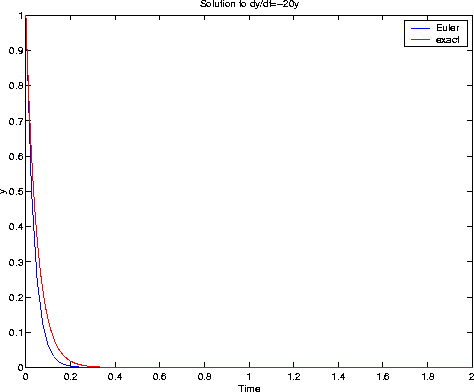
h=0.11

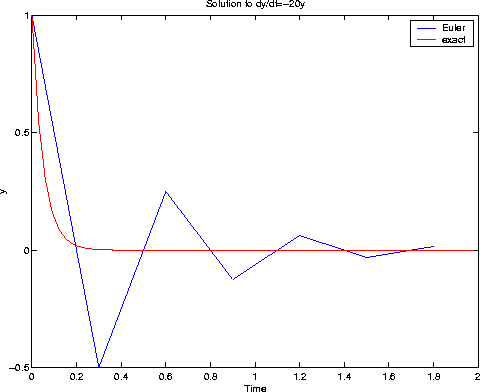
In all cases, the solution behaves correctly qualitatively, i.e., it decays.
In fact, we can use arbitrarily large timesteps to get the correct qualitative behaviour.
This is why the method is called A-stable. The region of stability is the entire
left half plane.
h=0.3
h=0.11
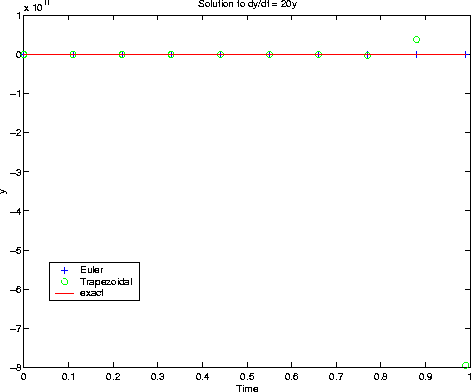
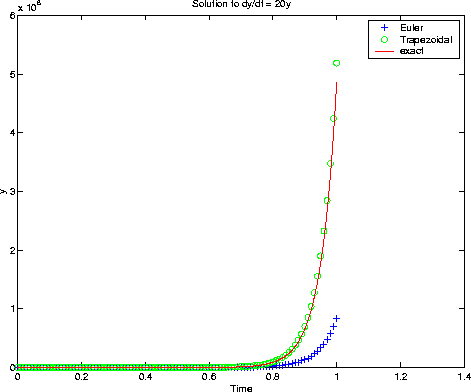
What do we learn: With both methods, and the timesteps chosen, the results
are not particularly good. But: the qualitative behaviour is correct,
in the sense that the solution grows.
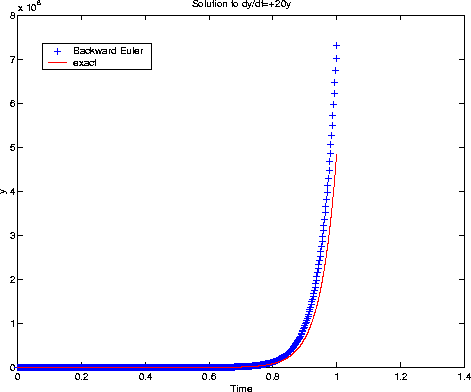
h=0.11
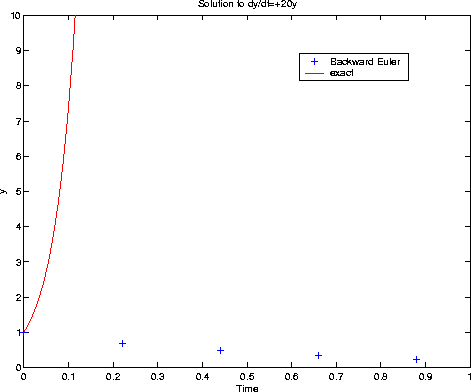
Clearly, the qualitative behaviour is wrong for h=0.11. This is so because
20*h is in the region of absolute stability!!