Problem 2
Describe explicitly all inner products on
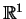 and on
and on
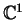 .
.
b) Let
Problem 3
a) Let 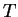 be the linear operator on
be the linear operator on
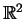 defined by
defined by
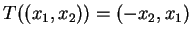 (that is,
(that is, 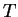 is rotation by
is rotation by 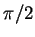 ).
Find all inner products
).
Find all inner products
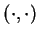 on
on
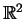 such
that
such
that
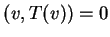 for all
for all
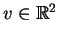 . (Hint: start
by noticing that the standard inner product
. (Hint: start
by noticing that the standard inner product
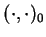 satisfies
this condition).
satisfies
this condition).